Computational Considerations :: Matrices and Linear Algebra (Mathematics)

Mathematics

Computational Considerations

One of the most important problems in technical computing is the solution of simultaneous linear equations. In matrix notation, this problem can be stated as follows.

Given two matrices A and B, does there exist a unique matrix X so that AX = B or XA = B?

It is instructive to consider a 1-by-1 example.

Does the equation

have a unique solution ?

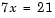
The answer, of course, is yes. The equation has the unique solution x = 3. The solution is easily obtained by division.

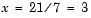
The solution is not ordinarily obtained by computing the inverse of 7, that is 7^-1 = 0.142857..., and then multiplying 7^-1 by 21. This would be more work and, if 7^-1 is represented to a finite number of digits, less accurate. Similar considerations apply to sets of linear equations with more than one unknown;
MATLAB solves such equations without computing the inverse of the matrix.

Although it is not standard mathematical notation, MATLAB uses the division terminology familiar in the scalar case to describe the solution of a general system of simultaneous equations. The two division symbols, slash, /, and backslash, \, are used for the two situations where the unknown matrix appears on the left or right of the coefficient matrix.

X = A\B
Denotes the solution to the matrix equation AX = B.

X = B/A
Denotes the solution to the matrix equation XA = B.

`X = A\B`	Denotes the solution to the matrix equation AX = B.
`X = B/A`	Denotes the solution to the matrix equation XA = B.

You can think of "dividing" both sides of the equation AX = B or XA = B by A. The coefficient matrix A is always in the "denominator."

The dimension compatibility conditions for X = A\B require the two matrices A and B to have the same number of rows. The solution X then has the same number of columns as B and its row dimension is equal to the column dimension of A. For X = B/A, the roles of rows and columns are interchanged.

In practice, linear equations of the form AX = B occur more frequently than those of the form XA = B. Consequently, backslash is used far more frequently than slash. The remainder of this section concentrates on the backslash operator; the corresponding properties of the slash operator can be inferred from the identity

```
(B/A)' = (A'\B')
```

The coefficient matrix A need not be square. If A is m-by-n, there are three cases.

m = n

Square system. Seek an exact solution.

m > n

Overdetermined system. Find a least squares solution.

m < n

Underdetermined system. Find a basic solution with at most m nonzero components.

m = n	Square system. Seek an exact solution.
m > n	Overdetermined system. Find a least squares solution.
m < n	Underdetermined system. Find a basic solution with at most m nonzero components.

The backslash operator employs different algorithms to handle different kinds of coefficient matrices. The various cases, which are diagnosed automatically by examining the coefficient matrix, include:

Permutations of triangular matrices
Symmetric, positive definite matrices
Square, nonsingular matrices
Rectangular, overdetermined systems
Rectangular, underdetermined systems

Solving Linear Systems of Equations General Solution