MATLAB Function Reference

deval

Evaluate the solution of a differential equation

Syntax

• sxint = deval(sol,xint)
  sxint = deval(xint,sol)
  sxint = deval(sol,xint,idx)
  sxint = deval(xint,sol,idx)
  [sxint, spxint] = deval(...)
  

Description

sxint = deval(sol,xint) and sxint = deval(xint,sol) evaluate the solution of a differential equation problem. sol is a structure returned by one of these solvers:

• An initial value problem solver (ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb, ode15i)
• The delay differential equations solver (dde23),
• The boundary value problem solver (bvp4c).

xint is a point or a vector of points at which you want the solution. The elements of xint must be in the interval [sol.x(1),sol.x(end)]. For each i, sxint(:,i) is the solution at xint(i).

sxint = deval(sol,xint,idx) and sxint = deval(xint,sol,idx) evaluate as above but return only the solution components with indices listed in the vector idx.

[sxint, spxint] = deval(...) also returns spxint, the value of the first derivative of the polynomial interpolating the solution.

Note    For multipoint boundary value problems, the solution obtained by bvp4c might be discontinuous at the interfaces. For an interface point xc, deval returns the average of the limits from the left and right of xc. To get the limit values, set the xint argument of deval to be slightly smaller or slightly larger than xc.

Example

This example solves the system 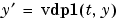using ode45, and evaluates and plots the first component of the solution at 100 points in the interval [0,20].

• sol = ode45(@vdp1,[0 20],[2 0]);
  x = linspace(0,20,100);
  y = deval(sol,x,1);
  plot(x,y);
  
  
  

See Also

ODE solvers: ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb, ode15i

DDE solver: dde23

BVP solver: bvp4c

detrend

diag

© 1994-2005 The MathWorks, Inc.