

| MATLAB Function Reference |   |
Find eigenvalues and eigenvectors
Syntax
d = eig(A)
d = eig(A,B)
[V,D] = eig(A)
[V,D] = eig(A,'nobalance')
[V,D] = eig(A,B)
[V,D] = eig(A,B,flag)
Description
d = eig(A)
returns a vector of the eigenvalues of matrix A.
d = eig(A,B)
returns a vector containing the generalized eigenvalues, if A and B are square matrices.
Note
If S is sparse and symmetric, you can use d = eig(S) to returns the eigenvalues of S. If S is sparse but not symmetric, or if you want to return the eigenvectors of S, use the function eigs instead of eig.
|
[V,D] = eig(A)
produces matrices of eigenvalues (D) and eigenvectors (V) of matrix A, so that A*V = V*D. Matrix D is the canonical form of A--a diagonal matrix with A's eigenvalues on the main diagonal. Matrix V is the modal matrix--its columns are the eigenvectors of A.
If W is a matrix such that W'*A = D*W', the columns of W are the left eigenvectors of A. Use [W,D] = eig(A.'); W = conj(W) to compute the left eigenvectors.
[V,D] = eig(A,'nobalance')
finds eigenvalues and eigenvectors without a preliminary balancing step. Ordinarily, balancing improves the conditioning of the input matrix, enabling more accurate computation of the eigenvectors and eigenvalues. However, if a matrix contains small elements that are really due to roundoff error, balancing may scale them up to make them as significant as the other elements of the original matrix, leading to incorrect eigenvectors. Use the nobalance option in this event. See the balance function for more details.
[V,D] = eig(A,B)
produces a diagonal matrix D of generalized eigenvalues and a full matrix V whose columns are the corresponding eigenvectors so that A*V = B*V*D.
[V,D] = eig(A,B, specifies the algorithm used to compute eigenvalues and eigenvectors. flag)
flag can be:
Note
For eig(A), the eigenvectors are scaled so that the norm of each is 1.0. For eig(A,B), eig(A,'nobalance'), and eig(A,B,flag), the eigenvectors are not normalized.
|
Remarks
The eigenvalue problem is to determine the nontrivial solutions of the equation
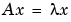
where 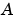 is an
is an n-by-n matrix, 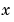 is a length
is a length n column vector, and 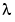 is a scalar. The
is a scalar. The n values of 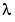 that satisfy the equation are the eigenvalues, and the corresponding values of
that satisfy the equation are the eigenvalues, and the corresponding values of 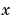 are the right eigenvectors. In MATLAB, the function
are the right eigenvectors. In MATLAB, the function eig solves for the eigenvalues 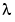 , and optionally the eigenvectors
, and optionally the eigenvectors 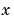 .
.
The generalized eigenvalue problem is to determine the nontrivial solutions of the equation
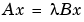
where both 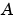 and
and 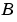 are
are n-by-n matrices and  is a scalar. The values of
is a scalar. The values of 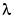 that satisfy the equation are the generalized eigenvalues and the corresponding values of
that satisfy the equation are the generalized eigenvalues and the corresponding values of 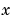 are the generalized right eigenvectors.
are the generalized right eigenvectors.
If 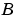 is nonsingular, the problem could be solved by reducing it to a standard eigenvalue problem
is nonsingular, the problem could be solved by reducing it to a standard eigenvalue problem
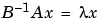
Because 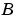 can be singular, an alternative algorithm, called the QZ method, is necessary.
can be singular, an alternative algorithm, called the QZ method, is necessary.
When a matrix has no repeated eigenvalues, the eigenvectors are always independent and the eigenvector matrix V diagonalizes the original matrix A if applied as a similarity transformation. However, if a matrix has repeated eigenvalues, it is not similar to a diagonal matrix unless it has a full (independent) set of eigenvectors. If the eigenvectors are not independent then the original matrix is said to be defective. Even if a matrix is defective, the solution from eig satisfies A*X = X*D.
Examples
has elements on the order of roundoff error. It is an example for which the nobalance option is necessary to compute the eigenvectors correctly. Try the statements
Inputs of Type Double
For inputs of type double, MATLAB uses the following LAPACK routines to compute eigenvalues and eigenvectors.
Inputs of Type Single
For inputs of type single, MATLAB uses the following LAPACK routines to compute eigenvalues and eigenvectors.
See Also
balance, condeig, eigs, hess, qz, schur
References
[1] Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide (http://www.netlib.org/lapack/lug/ lapack_lug.html), Third Edition, SIAM, Philadelphia, 1999.
 | edit | eigs |  |
© 1994-2005 The MathWorks, Inc.