

| MATLAB Function Reference |   |
Syntax
Description
The norm of a matrix is a scalar that gives some measure of the magnitude of the elements of the matrix. The norm function calculates several different types of matrix norms:
n = norm(A)
returns the largest singular value of A, max(svd(A)).
n = norm(A,p)
returns a different kind of norm, depending on the value of p.
norm(A,p) |
Returns sum(abs(A).^p)^(1/p), for any 1 <= p <= 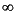 . . |
norm(A) |
Returns norm(A,2). |
|
Returns max(abs(A)). |
|
Returns min(abs(A)). |
Remarks
Note that norm(x) is the Euclidean length of a vector x. On the other hand, MATLAB uses "length" to denote the number of elements n in a vector. This example uses norm(x)/sqrt(n) to obtain the root-mean-square (RMS) value of an n-element vector x.
x = [0 1 2 3] x = 0 1 2 3 sqrt(0+1+4+9) % Euclidean length ans = 3.7417 norm(x) ans = 3.7417 n = length(x) % Number of elements n = 4 rms = 3.7417/2 % rms = norm(x)/sqrt(n) rms = 1.8708
See Also
cond, condest, normest, rcond, svd
 | nonzeros | normest |  |
© 1994-2005 The MathWorks, Inc.