residue (MATLAB Functions)

Convert between partial fraction expansion and polynomial coefficients

Syntax

[r,p,k] = residue(b,a)
[b,a] = residue(r,p,k)

Description

The residue function converts a quotient of polynomials to pole-residue representation, and back again.

[r,p,k] = residue(b,a) 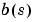finds the residues, poles, and direct term of a partial fraction expansion of the ratio of two polynomials, and 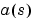, of the form

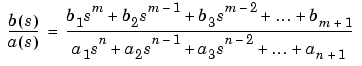
where 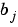and 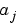are the jth elements of the input vectors b and a.

[b,a] = residue(r,p,k) converts the partial fraction expansion back to the polynomials with coefficients in b and a.

Definition

If there are no multiple roots, then

The number of poles n is

n = length(a)-1 = length(r) = length(p)

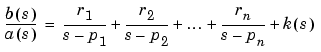
The direct term coefficient vector is empty if length(b) < length(a); otherwise

```
length(k) = length(b)-length(a)+1
```

If p(j) = ... = p(j+m-1) is a pole of multiplicity m, then the expansion includes terms of the form

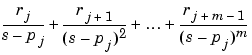
Arguments

b,a
Vectors that specify the coefficients of the polynomials in descending powers of

r
Column vector of residues

p
Column vector of poles

k
Row vector of direct terms

`b,a`	Vectors that specify the coefficients of the polynomials in descending powers of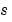
`r`	Column vector of residues
`p`	Column vector of poles
`k`	Row vector of direct terms

Algorithm

It first obtains the poles with roots. Next, if the fraction is nonproper, the direct term k is found using deconv, which performs polynomial long division. Finally, the residues are determined by evaluating the polynomial with individual roots removed. For repeated roots, resi2 computes the residues at the repeated root locations.

Limitations

Numerically, the partial fraction expansion of a ratio of polynomials represents an ill-posed problem. If the denominator polynomial, 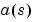, is near a polynomial with multiple roots, then small changes in the data, including roundoff errors, can make arbitrarily large changes in the resulting poles and residues. Problem formulations making use of state-space or zero-pole representations are preferable.

Examples

If the ratio of two polynomials is expressed as

then

```
b = [ 5 3 -2 7]
a = [-4 0 8 3]
```

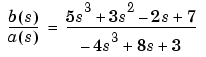
and you can calculate the partial fraction expansion as

[r, p, k] = residue(b,a)

r =
   -1.4167
   -0.6653
    1.3320

p =
    1.5737
   -1.1644
   -0.4093

k =
   -1.2500

Now, convert the partial fraction expansion back to polynomial coefficients.

[b,a] = residue(r,p,k)

b =
   -1.2500   -0.7500    0.5000   -1.7500

a =
    1.0000   -0.0000   -2.0000   -0.7500

The result can be expressed as

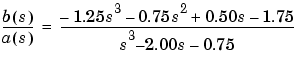
Note that the result is normalized for the leading coefficient in the denominator.

See Also

deconv, poly, roots

References

[1] Oppenheim, A.V. and R.W. Schafer, Digital Signal Processing, Prentice-Hall, 1975, p. 56.

reshape restoredefaultpath