MATLAB Function Reference

sort

Sort array elements in ascending or descending order

Syntax

• B = sort(A)
  B = sort(A,dim)
  B = sort(...,mode)
  [B,IX] = sort(...)
  

Description

B = sort(A) sorts the elements along different dimensions of an array, and arranges those elements in ascending order.

If A is a ...	sort(A) ...
Vector	Sorts the elements of A.
Matrix	Sorts each column of A.
Multidimensional array	Sorts A along the first non-singleton dimension, and returns an array of sorted vectors.
Cell array of strings	Sorts the strings in ASCII dictionary order.

Integer, real, logical, and character arrays are permitted. Floating-point arrays can be complex. For elements of A with identical values, the order of these elements is preserved in the sorted list. When A is complex, the elements are sorted by magnitude, i.e., abs(A), and where magnitudes are equal, further sorted by phase angle, i.e., angle(A), on the interval 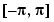. If A includes any NaN elements, sort places these at the high end.

B = sort(A,dim) sorts the elements along the dimension of A specified by a scalar dim.

B = sort(...,mode) sorts the elements in the specified direction, depending on the value of mode.

'ascend'	Ascending order (default)
'descend'	Descending order

[B,IX] = sort(A,...) also returns an array of indices IX, where size(IX) == size(A). If A is a vector, B = A(IX). If A is an m-by-n matrix, then each column of IX is a permutation vector of the corresponding column of A, such that

• for j = 1:n
      B(:,j) = A(IX(:,j),j); 
  end
  

If A has repeated elements of equal value, the returned indices preserve the original ordering.

Sorting Complex Entries

If A has complex entries r and s, sort orders them according to the following rule: r appears before s in sort(A) if either of the following hold:

• abs(r) < abs(s)
• abs(r) = abs(s) and angle(r)<angle(s)

• where

For example,

• v = [1 -1 i -i];
  angle(v)
  
  ans =
  
           0    3.1416    1.5708   -1.5708
  sort(v)
  
  ans =
  
          0 - 1.0000i   1.0000                  0 + 1.0000i  -1.0000
  

Note    sort uses a different rule for ordering complex numbers than do max and min, or the relational operators < and >. See the Relational Operators reference page for more information.

Examples

Example 1. This example sorts a matrix A in each dimension, and then sorts it a third time, requesting an array of indices for the sorted result.

• A = [ 3 7 5
        0 4 2 ];
  
  sort(A,1)
  
  ans =
       0     4     2
       3     7     5
  
  sort(A,2)
  
  ans =
       3     5     7
       0     2     4
  
  [B,IX] = sort(A,2)
  
  B =
       3     5     7
       0     2     4
  
  IX =
       1     3     2
       1     3     2
  

Example 2. This example sorts each column of a matrix in descending order.

• A = [ 3  7  5
        6  8  3
        0  4  2 ];
  
  sort(A,1,'descend')
  
  ans =
       6   8   5
       3   7   3
       0   4   2
  

This is equivalent to

• sort(A,'descend')
  
  ans =
       6   8   5
       3   7   3
       0   4   2
  

See Also

issorted, max, mean, median, min, sortrows

smooth3

sortrows

© 1994-2005 The MathWorks, Inc.