| Image Processing Toolbox User's Guide |
  |
bwmorph
Perform morphological operations on binary images
Syntax
Description
BW2 = bwmorph(BW,operation) applies a specific morphological operation to the binary image BW.
BW2 = bwmorph(BW,operation,n) applies the operation n times. n can be Inf, in which case the operation is repeated until the image no longer changes.
operation is a string that can have one of the values listed below.
Operation
|
Description
|
'bothat'
|
Performs the morphological "bottom hat" operation, which is closing (dilation followed by erosion) and subtracts the original image.
|
'bridge'
|
Bridges unconnected pixels, that is, sets 0-valued pixels to 1 if they have two nonzero neighbors that are not connected. For example:
|
'clean'
|
Removes isolated pixels (individual 1's that are surrounded by 0's), such as the center pixel in this pattern.
|
'close'
|
Performs morphological closing (dilation followed by erosion).
|
'diag'
|
Uses diagonal fill to eliminate 8-connectivity of the background. For example:
|
'dilate'
|
Performs dilation using the structuring element ones(3).
|
'erode'
|
Performs erosion using the structuring element ones(3)
|
'fill'
|
Fills isolated interior pixels (individual 0's that are surrounded by 1's), such as the center pixel in this pattern.
|
'hbreak'
|
Removes H-connected pixels. For example:
|
'majority'
|
Sets a pixel to 1 if five or more pixels in its 3-by-3 neighborhood are 1's; otherwise, it sets the pixel to 0.
|
'open'
|
Peforms morphological opening (erosion followed by dilation).
|
'remove'
|
Removes interior pixels. This option sets a pixel to 0 if all its 4-connected neighbors are 1, thus leaving only the boundary pixels on.
|
'shrink'
|
With n = Inf, shrinks objects to points. It removes pixels so that objects without holes shrink to a point, and objects with holes shrink to a connected ring halfway between each hole and the outer boundary. This option preserves the Euler number
|
'skel'
|
With n = Inf, removes pixels on the boundaries of objects but does not allow objects to break apart. The pixels remaining make up the image skeleton. This option preserves the Euler number.
|
'spur'
|
Removes spur pixels. For example:
|
'thicken'
|
With n = Inf, thickens objects by adding pixels to the exterior of objects until doing so would result in previously unconnected objects being 8-connected. This option preserves the Euler number.
|
'thin'
|
With n = Inf, thins objects to lines. It removes pixels so that an object without holes shrinks to a minimally connected stroke, and an object with holes shrinks to a connected ring halfway between each hole and the outer boundary. This option preserves the Euler number
|
'tophat'
|
Performs morphological "top hat" operation, returning the image minus the morphological opening of the image.
|
Class Support
The input image BW can be numeric or logical. It must be 2-D, real and nonsparse. The output image BW2 is of class logical.
Example
BW = imread('circles.png');
imshow(BW);
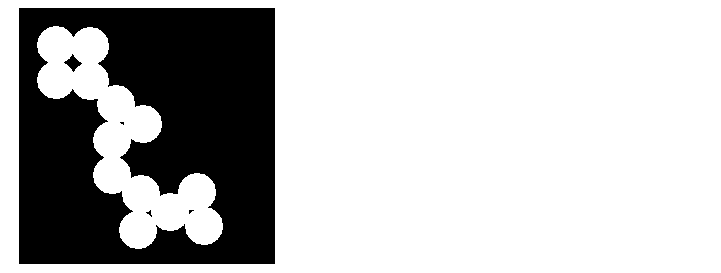
BW2 = bwmorph(BW,'remove');
figure, imshow(BW2)
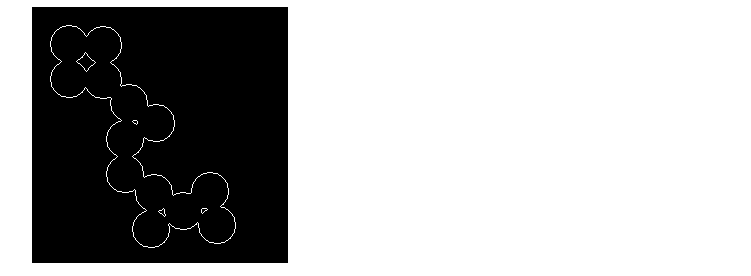
BW3 = bwmorph(BW,'skel',Inf);
figure, imshow(BW3)
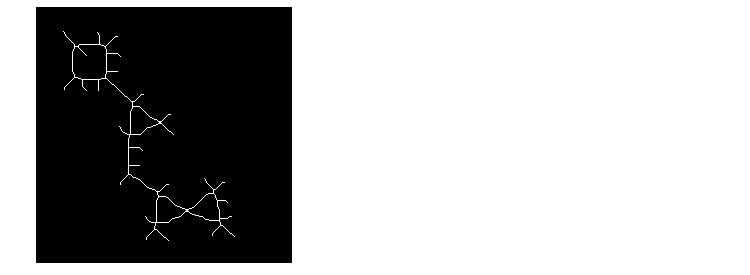
See Also
bweuler, bwperim, imdilate, imerode
References
[1] Haralick, Robert M., and Linda G. Shapiro, Computer and Robot Vision,
Volume I, Addison-Wesley, 1992.
[2] Pratt, William K., Digital Image Processing, John Wiley & Sons, Inc., 1991.
[3] Lam, L., Seong-Whan Lee, and Ching Y. Suen, "Thinning Methodologies-A
Comprehensive Survey," IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol 14, No. 9, September 1992, page 879, bottom of first column
through top of second column.
 | bwlabeln | | bwpack |  |
© 1994-2005 The MathWorks, Inc.





