ftrans2 (Image Processing Toolbox User's Guide)

Image Processing Toolbox User's Guide

Design two-dimensional FIR filter using frequency transformation

Syntax

```
h = ftrans2(b,t)
h = ftrans2(b)
```

Description

h = ftrans2(b,t) produces the two-dimensional FIR filter h that corresponds to the one-dimensional FIR filter b using the transform t. (ftrans2 returns h as a computational molecule, which is the appropriate form to use with filter2.) b must be a one-dimensional, odd-length (Type I) FIR filter such
as can be returned by fir1, fir2, or remez in the Signal Processing Toolbox. The transform matrix t contains coefficients that define the frequency
transformation to use. If t is m-by-n and b has length Q, then h is size
((m-1)*(Q-1)/2+1)-by-((n-1)*(Q-1)/2+1).

h = ftrans2(b) uses the McClellan transform matrix t.

```
t = [1 2 1; 2 -4 2; 1 2 1]/8;
```

Remarks

The transformation below defines the frequency response of the two-dimensional filter returned by ftrans2,

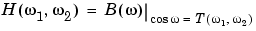
where B(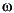) is the Fourier transform of the one-dimensional filter b,

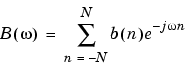
and T(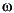₁,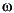₂) is the Fourier transform of the transformation matrix t.

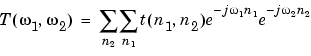
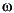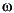The returned filter h is the inverse Fourier transform of H(₁,₂).

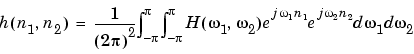
Example

Use ftrans2 to design an approximately circularly symmetric two-dimensional bandpass filter with passband between 0.1 and 0.6 (normalized frequency, where 1.0 corresponds to half the sampling frequency, or radians):

Since ftrans2 transforms a one-dimensional FIR filter to create a two-dimensional filter, first design a one-dimensional FIR bandpass filter using the Signal Processing Toolbox function remez.

colormap(jet(64))
b = remez(10,[0 0.05 0.15 0.55 0.65 1],[0 0 1 1 0 0]);
[H,w] = freqz(b,1,128,'whole');
plot(w/pi-1,fftshift(abs(H)))

Use ftrans2 with the default McClellan transformation to create the desired approximately circularly symmetric filter.

```
h = ftrans2(b);
freqz2(h)
```

See Also

conv2, filter2, fsamp2, fwind1, fwind2

Reference

[1] Lim, Jae S., Two-Dimensional Signal and Image Processing, Englewood Cliffs, NJ, Prentice Hall, 1990, pp. 218-237.

fspecial fwind1