Simulation Functions :: Advanced Topics (Neural Network Toolbox)

Neural Network Toolbox

Simulation Functions

You can create three kinds of simulation functions: transfer, net input, and weight functions. You can also provide associated derivative functions to enable backpropagation learning with your functions.

Transfer Functions

Transfer functions calculate a layer's output vector (or matrix) A, given its net input vector (or matrix) N. The only constraint on the relationship between the output and net input is that the output must have the same dimensions as the input.

Once defined, you can assign your transfer function to any layer of a network. For example, the following line of code assigns the transfer function yourtf to the second layer of a network.

```
net.layers{2}.transferFcn = 'yourtf';
```

Your transfer function then is used whenever you simulate your network.

```
[Y,Pf,Af] = sim(net,P,Pi,Ai)
```

To be a valid transfer function, your function must calculate outputs A from net inputs N as follows,

```
A = yourtf(N)
```

where:

N is an S x Q matrix of Q net input (column) vectors.
A is an S x Q matrix of Q output (column) vectors.

Your transfer function must also provide information about itself, using this calling format,

```
info = yourtf(code)
```

where the correct information is returned for each of the following string codes:

'version' -- Returns the Neural Network Toolbox version (3.0).
'deriv' -- Returns the name of the associated derivative function.
'output' -- Returns the output range.
'active' -- Returns the active input range.

The toolbox contains an example custom transfer function called mytf. Enter the following lines of code to see how it is used.

help mytf
n = -5:.1:5;
a = mytf(n);
plot(n,a)
mytf('deriv')

Enter the following command to see how mytf is implemented.

```
type mytf
```

You can use mytf as a template to create your own transfer function.

Transfer Derivative Functions. If you want to use backpropagation with your custom transfer function, you need to create a custom derivative function for it. The function needs to calculate the derivative of the layer's output with respect to its net input,

```
dA_dN = yourdtf(N,A)
```

where:

N is an matrix of Q net input (column) vectors.
A is an 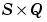matrix of Q output (column) vectors.
dA_dN is the 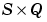derivative dA/dN.

This only works for transfer functions whose output elements are independent. In other words, where each A(i) is only a function of N(i). Otherwise, a three-dimensional array is required to store the derivatives in the case of multiple vectors (instead of a matrix as defined above). Such 3-D derivatives are not supported at this time.

To see how the example custom transfer derivative function mydtf works, type

help mydtf
da_dn = mydtf(n,a)
subplot(2,1,1), plot(n,a)
subplot(2,1,2), plot(n,dn_da)

Use this command to see how mydtf was implemented.

```
type mydtf
```

You can use mydtf as a template to create your own transfer derivative functions.

Net Input Functions

Net input functions calculate a layer's net input vector (or matrix) N, given its weighted input vectors (or matrices) Zi. The only constraints on the relationship between the net input and the weighted inputs are that the net input must have the same dimensions as the weighted inputs, and that the function cannot be sensitive to the order of the weight inputs.

Once defined, you can assign your net input function to any layer of a network. For example, the following line of code assigns the transfer function yournif to the second layer of a network.

```
net.layers{2}.netInputFcn = 'yournif';
```

Your net input function then is used whenever you simulate your network.

```
[Y,Pf,Af] = sim(net,P,Pi,Ai)
```

To be a valid net input function your function must calculate outputs A from net inputs N as follows,

```
N = yournif(Z1,Z2,...)
```

where

Zi is the ith 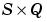matrix of Q weighted input (column) vectors.
N is an matrix of Q net input (column) vectors.

Your net input function must also provide information about itself using this calling format,

```
info = yournif(code)
```

where the correct information is returned for each of the following string codes:

'version' -- Returns the Neural Network Toolbox version (3.0).
'deriv' -- Returns the name of the associated derivative function.

The toolbox contains an example custom net input function called mynif. Enter the following lines of code to see how it is used.

help mynif
z1 = rand(4,5);
z2 = rand(4,5);
z3 = rand(4,5);
n = mynif(z1,z2,z3)
mynif('deriv')

Enter the following command to see how mynif is implemented.

```
type mynif
```

You can use mynif as a template to create your own net input function.

Net Input Derivative Functions. If you want to use backpropagation with your custom net input function, you need to create a custom derivative function for it. It needs to calculate the derivative of the layer's net input with respect to any of its weighted inputs,

```
dN_dZ = dtansig(Z,N)
```

where:

Z is one of the 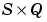matrices of Q weighted input (column) vectors.
N is an matrix of Q net input (column) vectors.
dN_dZ is the 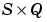derivative dN/dZ.

To see how the example custom net input derivative function mydtf works, type

help mydnif
dn_dz1 = mydnif(z1,n)
dn_dz2 = mydnif(z1,n)
dn_dz3 = mydnif(z1,n)

Use this command to see how mydtf was implemented.

```
type mydnif
```

You can use mydnif as a template to create your own net input derivative functions.

Weight Functions

Weight functions calculate a weighted input vector (or matrix) Z, given an input vector (or matrices) P and a weight matrix W.

Once defined, you can assign your weight function to any input weight or layer weight of a network. For example, the following line of code assigns the weight function yourwf to the weight going to the second layer from the first input of a network.

net.inputWeights{2,1}.weightFcn = 'yourwf';

Your weight function is used whenever you simulate your network.

```
[Y,Pf,Af] = sim(net,P,Pi,Ai)
```

To be a valid weight function your function must calculate weight inputs Z from inputs P and a weight matrix W as follows,

```
Z = yourwf(W,P)
```

where:

W is an 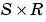weight matrix.
P is an matrix of Q input (column) vectors.
Z is an matrix of Q weighted input (column) vectors.

Your net input function must also provide information about itself using this calling format,

```
info = yourwf(code)
```

where the correct information is returned for each of the following string codes:

'version' -- Returns the Neural Network Toolbox version (3.0).
'deriv' -- Returns the name of the associated derivative function.

The toolbox contains an example custom weight called mywf. Enter the following lines of code to see how it is used.

help mywf
w = rand(1,5);
p = rand(5,1);
z = mywf(w,p);
mywf('deriv')

Enter the following command to see how mywf is implemented.

```
type mywf
```

You can use mywf as a template to create your own weight functions.

Weight Derivative Functions. If you want to use backpropagation with your custom weight function, you need to create a custom derivative function for it. It needs to calculate the derivative of the weight inputs with respect to both the input and weight,

dZ_dP = mydwf('p',W,P,Z)
dZ_dW = mydwf('w',W,P,Z)

where:

W is an weight matrix.
P is an 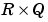matrix of Q input (column) vectors.
Z is an 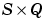matrix of Q weighted input (column) vectors.
dZ_dP is the 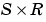derivative dZ/dP.
dZ_dW is the 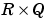derivative dZ/dW.

This only works for weight functions whose output consists of a sum of i term, where each ith term is a function of only W(i) and P(i). Otherwise a three-dimensional array is required to store the derivatives in the case of multiple vectors (instead of a matrix as defined above). Such 3-D derivatives are not supported at this time.

To see how the example custom net input derivative function mydwf works, type

help mydwf
dz_dp = mydwf('p',w,p,z)
dz_dw = mydwf('w',w,p,z)

Use this command to see how mydwf is implemented.

```
type mydwf
```

You can use mydwf as a template to create your own net input derivative function.

Custom Functions Initialization Functions