Learning Functions :: Advanced Topics (Neural Network Toolbox)

Neural Network Toolbox

Learning Functions

You can create four kinds of initialization functions: training, adaption, performance, and weight/bias learning.

Training Functions

One kind of general learning function is a network training function. Training functions repeatedly apply a set of input vectors to a network, updating the network each time, until some stopping criterion is met. Stopping criteria can consist of a maximum number of epochs, a minimum error gradient, an error goal, etc.

Once defined, you can assign your training function to a network.

```
net.trainFcn = 'yourtf';
```

Your network initialization function is used whenever you train your network.

```
[net,tr] = train(NET,P,T,Pi,Ai)
```

To be a valid training function your function must take and return a network,

[net,tr] = yourtf(net,Pd,Tl,Ai,Q,TS,VV,TV)

where:

Pd is an 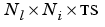cell array of tap delayed inputs.

Each Pd{i,j,ts} is the 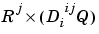delayed input matrix to the weight going to the ith layer from the jth input at time step ts. (Pd{i,j,ts} is an empty matrix [] if the ith layer doesn't have a weight from the jth input.)

Tl is an 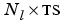cell array of layer targets.

Each Tl{i,ts} is the 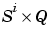target matrix for the ith layer. (Tl{i,ts} is an empty matrix if the ith layer doesn't have a target.)

Ai is an 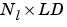cell array of initial layer delay states.

Each Ai{l,k} is the delayed ith layer output for time step ts = k-LD, where ts goes from 0 to LD-1.

Q is the number of concurrent vectors.
TS is the number of time steps.
VV and TV are optional structures defining validation and test vectors in the same form as the training vectors defined above: Pd, Tl, Ai, Q, and TS. Note that the validation and testing Q and TS values can be different from each other and from those used by the training vectors.

The dimensions above have the following definitions:

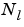is the number of network layers (net.numLayers).
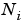is the number of network inputs (net.numInputs).
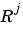is the size of the jth input (net.inputs{j}.size).
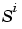is the size of the ith layer (net.layers{i}.size)
LD is the number of layer delays (net.numLayerDelays).
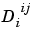is the number of delay lines associated with the weight going to the ith layer from the jth input (length(net.inputWeights{i,j}.delays)).

Your training function must also provide information about itself using this calling format,

```
info = yourtf(code)
```

where the correct information is returned for each of the following string codes:

'version' -- Returns the Neural Network Toolbox version (3.0).
'pdefaults' -- Returns a structure of default training parameters.

When you set the network training function (net.trainFcn) to be your function, the network's training parameters (net.trainParam) automatically are set to your default structure. Those values can be altered (or not) before training.

Your function can update the network's weight and bias values in any way you see fit. However, you should be careful not to alter any other properties, or to set the weight matrices and bias vectors to the wrong size. For performance reasons, train turns off the normal type checking for network properties before calling your training function. So if you set a weight matrix to the wrong size, it won't immediately generate an error, but will cause problems later when you try to simulate or adapt the network.

If you are interested in creating your own training function, you can examine the implementations of toolbox functions such as trainc and trainr. The help for each of these utility functions lists the input and output arguments they take.

Utility Functions. If you examine training functions such as trainc, traingd, and trainlm, note that they use a set of utility functions found in the nnet/nnutils directory.

These functions are not listed in Reference because they may be altered in the future. However, you can use these functions if you are willing to take the risk that you might have to update your functions for future versions of the toolbox. Use help on each function to view the function's input and output arguments.

These two functions are useful for creating a new training record and truncating it once the final number of epochs is known:

newtr -- New training record with any number of optional fields.
cliptr -- Clip training record to the final number of epochs.

These three functions calculate network signals going forward, errors, and derivatives of performance coming back:

calca -- Calculate network outputs and other signals.
calcerr -- Calculate matrix or cell array errors.
calcgrad -- Calculate bias and weight performance gradients.

These two functions get and set a network's weight and bias values with single vectors. Being able to treat all these adjustable parameters as a single vector is often useful for implementing optimization algorithms:

getx -- Get all network weight and bias values as a single vector.
setx -- Set all network weight and bias values with a single vector.

These next three functions are also useful for implementing optimization functions. One calculates all network signals going forward, including errors and performance. One backpropagates to find the derivatives of performance as a single vector. The third function backpropagates to find the Jacobian of performance. This latter function is used by advanced optimization techniques like Levenberg-Marquardt:

calcperf -- Calculate network outputs, signals, and performance.
calcgx -- Calculate weight and bias performance gradient as a single vector.
calcjx -- Calculate weight and bias performance Jacobian as a single matrix.

Adapt Functions

The other kind of the general learning function is a network adapt function. Adapt functions simulate a network, while updating the network for each time step of the input before continuing the simulation to the next input.

Once defined, you can assign your adapt function to a network.

```
net.adaptFcn = 'youraf';
```

Your network initialization function is used whenever you adapt your network.

```
[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)
```

To be a valid adapt function, it must take and return a network,

[net,Ac,El] = youraf(net,Pd,Tl,Ai,Q,TS)

where:

Pd is an 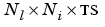cell array of tap delayed inputs.

Each Pd{i,j,ts} is the 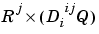delayed input matrix to the weight going to the ith layer from the jth input at time step ts. Note that (Pd{i,j,ts} is an empty matrix [] if the ith layer doesn't have a weight from the jth input.)

Tl is an 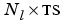cell array of layer targets.

Each Tl{i,ts} is the 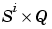target matrix for the ith layer. Note that (Tl{i,ts} is an empty matrix if the ith layer doesn't have a target.)

Ai is an 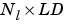cell array of initial layer delay states.

Each Ai{l,k} is the delayed ith layer output for time step ts = k-LD, where ts goes from 0 to LD-1.

Q is the number of concurrent vectors.
TS is the number of time steps.

The dimensions above have the following definitions:

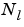is the number of network layers (net.numLayers).
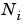is the number of network inputs (net.numInputs).
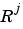is the size of the jth input (net.inputs{j}.size).
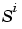is the size of the ith layer (net.layers{i}.size)
LD is the number of layer delays (net.numLayerDelays).
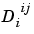is the number of delay lines associated with the weight going to the ith layer from the jth input (length(net.inputWeights{i,j}.delays)).

Your adapt function must also provide information about itself using this calling format,

```
info = youraf(code)
```

where the correct information is returned for each of the following string codes:

'version' -- Returns the Neural Network Toolbox version (3.0).
'pdefaults' -- Returns a structure of default adapt parameters.

When you set the network adapt function (net.adaptFcn) to be your function, the network's adapt parameters (net.adaptParam) automatically are set to your default structure. Those values can then be altered (or not) before adapting.

Your function can update the network's weight and bias values in any way you see fit. However, you should be careful not to alter any other properties, or to set the weight matrices and bias vectors of the wrong size. For performance reasons, adapt turns off the normal type checking for network properties before calling your adapt function. So if you set a weight matrix to the wrong size, it won't immediately generate an error, but will cause problems later when you try to simulate or train the network.

If you are interested in creating your own training function, you can examine the implementation of a toolbox function such as trains.

Utility Functions. If you examine the toolbox's only adapt function trains, note that it uses a set of utility functions found in the nnet/nnutils directory. The help for each of these utility functions lists the input and output arguments they take.

These functions are not listed in Reference because they may be altered in the future. However, you can use these functions if you are willing to take the risk that you will have to update your functions for future versions of the toolbox.

These two functions are useful for simulating a network, and calculating its derivatives of performance:

calca1 -- New training record with any number of optional fields.
calce1 -- Clip training record to the final number of epochs.
calcgrad -- Calculate bias and weight performance gradients.

Performance Functions

Performance functions allow a network's behavior to be graded. This is useful for many algorithms, such as backpropagation, which operate by adjusting network weights and biases to improve performance.

Once defined you can assign your training function to a network.

```
net.performFcn = 'yourpf';
```

Your network initialization function will then be used whenever you train your adapt your network.

[net,tr] = train(NET,P,T,Pi,Ai)
[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

To be a valid performance function your function must be called as follows,

```
perf = yourpf(E,X,PP)
```

where:

E is either an S x Q matrix or an 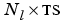cell array of layer errors.

Each E{i,ts} is the 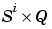target matrix for the ith layer. (Tl(i,ts) is an empty matrix if the ith layer doesn't have a target.)

X is an M x 1 vector of all the network's weights and biases.
PP is a structure of network performance parameters.

If E is a cell array you can convert it to a matrix as follows.

```
E = cell2mat(E);
```

Alternatively, your function must also be able to be called as follows,

```
perf = yourpf(E,net)
```

where you can get X and PP (if needed) as follows.

```
X = getx(net);
PP = net.performParam;
```

Your performance function must also provide information about itself using this calling format,

```
info = yourpf(code)
```

where the correct information is returned for each of the following string codes:

'version' -- Returns the Neural Network Toolbox version (3.0).
'deriv' -- Returns the name of the associated derivative function.
'pdefaults' -- Returns a structure of default performance parameters.

When you set the network performance function (net.performFcn) to be your function, the network's adapt parameters (net.performParam) are automatically set to your default structure. Those values can then be altered or not before training or adaption.

To see how an example custom performance function works type in these lines of code.

help mypf
e = rand(4,5);
x = rand(12,1);
pp = mypf('pdefaults')
perf = mypf(e,x,pp)

Use this command to see how mypf was implemented.

```
type mypf
```

You can use mypf as a template to create your own weight and bias initialization function.

Performance Derivative Functions. If you want to use backpropagation with your performance function, you need to create a custom derivative function for it. It needs to calculate the derivative of the network's errors and combined weight and bias vector, with respect to performance,

dPerf_dE = dmsereg('e',E,X,perf,PP)
dPerf_dX = dmsereg('x',E,X,perf,PP)

where:

E is an 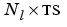cell array of layer errors.

Each E{i,ts} is the 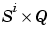target matrix for the ith layer. Note that (Tl(i,ts) is an empty matrix if the ith layer doesn't have a target.)

X is an 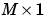vector of all the network's weights and biases.
PP is a structure of network performance parameters.
dPerf_dE is the 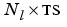cell array of derivatives dPerf/dE.

Each E{i,ts} i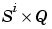s the derivative matrix for the ith layer. Note that (Tl(i,ts) is an empty matrix if the ith layer doesn't have a target.)

dPerf_dX is the 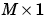derivative dPerf/dX.

To see how the example custom performance derivative function mydpf works, type

help mydpf
e = {e};
dperf_de = mydpf('e',e,x,perf,pp)
dperf_dx = mydpf('x',e,x,perf,pp)

Use this command to see how mydpf was implemented.

```
type mydpf
```

You can use mydpf as a template to create your own performance derivative functions.

Weight and Bias Learning Functions

The most specific kind of learning function is a weight and bias learning function. These functions are used to update individual weights and biases during learning with some training and adapt functions.

Once defined. you can assign your learning function to any weight and bias in a network. For example, the following lines of code assign the weight and bias learning function yourwblf to the second layer's bias, and the weight coming from the first input to the second layer.

net.biases{2}.learnFcn = 'yourwblf';
net.inputWeights{2,1}.learnFcn = 'yourwblf';

Weight and bias learning functions are only called to update weights and biases if the network training function (net.trainFcn) is set to trainb, trainc, or trainr, or if the network adapt function (net.adaptFcn) is set to trains. If this is the case, then your function is used to update the weight and biases it is assigned to whenever you train or adapt your network with train or adapt.

[net,tr] = train(NET,P,T,Pi,Ai)
[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

To be a valid weight and bias learning function, it must be callable as follows,

[dW,LS] = yourwblf(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)

where:

W is an 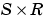weight matrix.
P is an 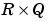matrix of Q input (column) vectors.
Z is an 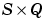matrix of Q weighted input (column) vectors.
N is an 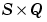matrix of Q net input (column) vectors.
A is an 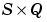matrix of Q layer output (column) vectors.
T is an 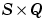matrix of Q target (column) vectors.
E is an 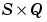matrix of Q error (column) vectors.
gW is an 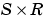gradient of W with respect to performance.
gA is an 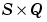gradient of A with respect to performance.
D is an 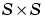matrix of neuron distances.
LP is a a structure of learning parameters.
LS is a structure of the learning state that is updated for each call. (Use a null matrix [] the first time.)
dW is the resulting 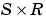weight change matrix.

Your function is called as follows to update bias vector

[db,LS] = yourwblf(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)

where:

S is the number of neurons in the layer.
b is a new bias vector.

Your learning function must also provide information about itself using this calling format,

```
info = yourwblf(code)
```

where the correct information is returned for each of the following string codes:

'version' -- Returns the Neural Network Toolbox version (3.0).
'deriv' -- Returns the name of the associated derivative function.
'pdefaults' -- Returns a structure of default performance parameters.

To see how an example custom weight and bias initialization function works, type

```
help mywblf
```

Use this command to see how mywbif was implemented.

```
type mywblf
```

You can use mywblf as a template to create your own weight and bias learning function.

Initialization Functions Self-Organizing Map Functions