Neural Network Toolbox

Training

Once the network weights and biases have been initialized, the network is ready for training. The network can be trained for function approximation (nonlinear regression), pattern association, or pattern classification. The training process requires a set of examples of proper network behavior - network inputs p and target outputs t. During training the weights and biases of the network are iteratively adjusted to minimize the network performance function net.performFcn. The default performance function for feedforward networks is mean square error mse - the average squared error between the network outputs a and the target outputs t.

The remainder of this chapter describes several different training algorithms for feedforward networks. All of these algorithms use the gradient of the performance function to determine how to adjust the weights to minimize performance. The gradient is determined using a technique called backpropagation, which involves performing computations backwards through the network. The backpropagation computation is derived using the chain rule of calculus and is described in Chapter 11 of [HDB96].

The basic backpropagation training algorithm, in which the weights are moved in the direction of the negative gradient, is described in the next section. Later sections describe more complex algorithms that increase the speed of convergence.

Backpropagation Algorithm

There are many variations of the backpropagation algorithm, several of which we discuss in this chapter. The simplest implementation of backpropagation learning updates the network weights and biases in the direction in which the performance function decreases most rapidly -- the negative of the gradient. One iteration of this algorithm can be written

where 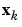is a vector of current weights and biases, 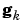is the current gradient, and 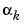is the learning rate.

There are two different ways in which this gradient descent algorithm can be implemented: incremental mode and batch mode. In the incremental mode, the gradient is computed and the weights are updated after each input is applied to the network. In the batch mode all of the inputs are applied to the network before the weights are updated. The next section describes the batch mode of training; incremental training will be discussed in a later chapter.

Batch Training (train).   In batch mode the weights and biases of the network are updated only after the entire training set has been applied to the network. The gradients calculated at each training example are added together to determine the change in the weights and biases. For a discussion of batch training with the backpropagation algorithm see page 12-7 of [HDB96].

Batch Gradient Descent (traingd).   The batch steepest descent training function is traingd. The weights and biases are updated in the direction of the negative gradient of the performance function. If you want to train a network using batch steepest descent, you should set the network trainFcn to traingd, and then call the function train. There is only one training function associated with a given network.

There are seven training parameters associated with traingd: epochs, show, goal, time, min_grad, max_fail, and lr. The learning rate lr is multiplied times the negative of the gradient to determine the changes to the weights and biases. The larger the learning rate, the bigger the step. If the learning rate is made too large, the algorithm becomes unstable. If the learning rate is set too small, the algorithm takes a long time to converge. See page 12-8 of [HDB96] for a discussion of the choice of learning rate.

The training status is displayed for every show iteration of the algorithm. (If show is set to NaN, then the training status never displays.) The other parameters determine when the training stops. The training stops if the number of iterations exceeds epochs, if the performance function drops below goal, if the magnitude of the gradient is less than mingrad, or if the training time is longer than time seconds. We discuss max_fail, which is associated with the early stopping technique, in the section on improving generalization.

The following code creates a training set of inputs p and targets t. For batch training, all of the input vectors are placed in one matrix.

• p = [-1 -1 2 2;0 5 0 5];
  t = [-1 -1 1 1];
  

Next, we create the feedforward network. Here we use the function minmax to determine the range of the inputs to be used in creating the network.

• net=newff(minmax(p),[3,1],{'tansig','purelin'},'traingd');
  

At this point, we might want to modify some of the default training parameters.

• net.trainParam.show = 50;
  net.trainParam.lr = 0.05;
  net.trainParam.epochs = 300;
  net.trainParam.goal = 1e-5;
  

If you want to use the default training parameters, the above commands are not necessary.

Now we are ready to train the network.

• [net,tr]=train(net,p,t);
     TRAINGD, Epoch 0/300, MSE 1.59423/1e-05, Gradient 
  2.76799/1e-10
     TRAINGD, Epoch 50/300, MSE 0.00236382/1e-05, Gradient 
  0.0495292/1e-10
     TRAINGD, Epoch 100/300, MSE 0.000435947/1e-05, Gradient 
  0.0161202/1e-10
     TRAINGD, Epoch 150/300, MSE 8.68462e-05/1e-05, Gradient 
  0.00769588/1e-10
     TRAINGD, Epoch 200/300, MSE 1.45042e-05/1e-05, Gradient 
  0.00325667/1e-10
     TRAINGD, Epoch 211/300, MSE 9.64816e-06/1e-05, Gradient 
  0.00266775/1e-10
     TRAINGD, Performance goal met.
  

The training record tr contains information about the progress of training. An example of its use is given in the Sample Training Session near the end of this chapter.

Now the trained network can be simulated to obtain its response to the inputs in the training set.

• a = sim(net,p)
  a =
     -1.0010   -0.9989    1.0018    0.9985
  

Try the Neural Network Design Demonstration nnd12sd1[HDB96] for an illustration of the performance of the batch gradient descent algorithm.

Batch Gradient Descent with Momentum (traingdm).   In addition to traingd, there is another batch algorithm for feedforward networks that often provides faster convergence - traingdm, steepest descent with momentum. Momentum allows a network to respond not only to the local gradient, but also to recent trends in the error surface. Acting like a low-pass filter, momentum allows the network to ignore small features in the error surface. Without momentum a network may get stuck in a shallow local minimum. With momentum a network can slide through such a minimum. See page 12-9 of [HDB96] for a discussion of momentum.

Momentum can be added to backpropagation learning by making weight changes equal to the sum of a fraction of the last weight change and the new change suggested by the backpropagation rule. The magnitude of the effect that the last weight change is allowed to have is mediated by a momentum constant, mc, which can be any number between 0 and 1. When the momentum constant is 0, a weight change is based solely on the gradient. When the momentum constant is 1, the new weight change is set to equal the last weight change and the gradient is simply ignored. The gradient is computed by summing the gradients calculated at each training example, and the weights and biases are only updated after all training examples have been presented.

If the new performance function on a given iteration exceeds the performance function on a previous iteration by more than a predefined ratio max_perf_inc (typically 1.04), the new weights and biases are discarded, and the momentum coefficient mc is set to zero.

The batch form of gradient descent with momentum is invoked using the training function traingdm. The traingdm function is invoked using the same steps shown above for the traingd function, except that the mc, lr and max_perf_inc learning parameters can all be set.

In the following code we recreate our previous network and retrain it using gradient descent with momentum. The training parameters for traingdm are the same as those for traingd, with the addition of the momentum factor mc and the maximum performance increase max_perf_inc. (The training parameters are reset to the default values whenever net.trainFcn is set to traingdm.)

• p = [-1 -1 2 2;0 5 0 5];
  t = [-1 -1 1 1];
  net=newff(minmax(p),[3,1],{'tansig','purelin'},'traingdm');
  net.trainParam.show = 50;
  net.trainParam.lr = 0.05;
  net.trainParam.mc = 0.9;
  net.trainParam.epochs = 300;
  net.trainParam.goal = 1e-5;
  [net,tr]=train(net,p,t);
     TRAINGDM, Epoch 0/300, MSE 3.6913/1e-05, Gradient 
  4.54729/1e-10
     TRAINGDM, Epoch 50/300, MSE 0.00532188/1e-05, Gradient 
  0.213222/1e-10
     TRAINGDM, Epoch 100/300, MSE 6.34868e-05/1e-05, Gradient 
  0.0409749/1e-10
     TRAINGDM, Epoch 114/300, MSE 9.06235e-06/1e-05, Gradient 
  0.00908756/1e-10
     TRAINGDM, Performance goal met.
  a = sim(net,p)
  a =
      -1.0026   -1.0044    0.9969    0.9992
  

Note that since we reinitialized the weights and biases before training (by calling newff again), we obtain a different mean square error than we did using traingd. If we were to reinitialize and train again using traingdm, we would get yet a different mean square error. The random choice of initial weights and biases will affect the performance of the algorithm. If you want to compare the performance of different algorithms, you should test each using several different sets of initial weights and biases. You may want to use net=init(net) to reinitialize the weights, rather than recreating the entire network with newff.

Try the Neural Network Design Demonstration nnd12mo [HDB96] for an illustration of the performance of the batch momentum algorithm.

Simulation (sim)

Faster Training

© 1994-2005 The MathWorks, Inc.