Neural Network Toolbox

Conjugate Gradient Algorithms

The basic backpropagation algorithm adjusts the weights in the steepest descent direction (negative of the gradient). This is the direction in which the performance function is decreasing most rapidly. It turns out that, although the function decreases most rapidly along the negative of the gradient, this does not necessarily produce the fastest convergence. In the conjugate gradient algorithms a search is performed along conjugate directions, which produces generally faster convergence than steepest descent directions. In this section, we present four different variations of conjugate gradient algorithms.

See page 12-14 of [HDB96] for a discussion of conjugate gradient algorithms and their application to neural networks.

In most of the training algorithms that we discussed up to this point, a learning rate is used to determine the length of the weight update (step size). In most of the conjugate gradient algorithms, the step size is adjusted at each iteration. A search is made along the conjugate gradient direction to determine the step size, which minimizes the performance function along that line. There are five different search functions included in the toolbox, and these are discussed at the end of this section. Any of these search functions can be used interchangeably with a variety of the training functions described in the remainder of this chapter. Some search functions are best suited to certain training functions, although the optimum choice can vary according to the specific application. An appropriate default search function is assigned to each training function, but this can be modified by the user.

Fletcher-Reeves Update (traincgf)

All of the conjugate gradient algorithms start out by searching in the steepest descent direction (negative of the gradient) on the first iteration.

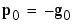
A line search is then performed to determine the optimal distance to move along the current search direction:

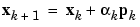
Then the next search direction is determined so that it is conjugate to previous search directions. The general procedure for determining the new search direction is to combine the new steepest descent direction with the previous search direction:

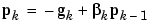
The various versions of conjugate gradient are distinguished by the manner in which the constant 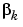is computed. For the Fletcher-Reeves update the procedure is

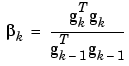
This is the ratio of the norm squared of the current gradient to the norm squared of the previous gradient.

See [FlRe64] or [HDB96] for a discussion of the Fletcher-Reeves conjugate gradient algorithm.

In the following code, we reinitialize our previous network and retrain it using the Fletcher-Reeves version of the conjugate gradient algorithm. The training parameters for traincgf are epochs, show, goal, time, min_grad, max_fail, srchFcn, scal_tol, alpha, beta, delta, gama, low_lim, up_lim, maxstep, minstep, bmax. We have previously discussed the first six parameters. The parameter srchFcn is the name of the line search function. It can be any of the functions described later in this section (or a user-supplied function). The remaining parameters are associated with specific line search routines and are described later in this section. The default line search routine srchcha is used in this example. traincgf generally converges in fewer iterations than trainrp (although there is more computation required in each iteration).

• p = [-1 -1 2 2;0 5 0 5];
  t = [-1 -1 1 1];
  net=newff(minmax(p),[3,1],{'tansig','purelin'},'traincgf');
  net.trainParam.show = 5;
  net.trainParam.epochs = 300;
  net.trainParam.goal = 1e-5;
  [net,tr]=train(net,p,t);
     TRAINCGF-srchcha, Epoch 0/300, MSE 2.15911/1e-05, Gradient 
  3.17681/1e-06
     TRAINCGF-srchcha, Epoch 5/300, MSE 0.111081/1e-05, Gradient 
  0.602109/1e-06
     TRAINCGF-srchcha, Epoch 10/300, MSE 0.0095015/1e-05, Gradient 
  0.197436/1e-06
     TRAINCGF-srchcha, Epoch 15/300, MSE 0.000508668/1e-05, 
  Gradient 0.0439273/1e-06
     TRAINCGF-srchcha, Epoch 17/300, MSE 1.33611e-06/1e-05, 
  Gradient 0.00562836/1e-06
     TRAINCGF, Performance goal met.
  a = sim(net,p)
  a =
     -1.0001   -1.0023    0.9999    1.0002
  

The conjugate gradient algorithms are usually much faster than variable learning rate backpropagation, and are sometimes faster than trainrp, although the results will vary from one problem to another. The conjugate gradient algorithms require only a little more storage than the simpler algorithms, so they are often a good choice for networks with a large number of weights.

Try the Neural Network Design Demonstration nnd12cg [HDB96] for an illustration of the performance of a conjugate gradient algorithm.

Polak-Ribiére Update (traincgp)

Another version of the conjugate gradient algorithm was proposed by Polak and Ribiére. As with the Fletcher-Reeves algorithm, the search direction at each iteration is determined by

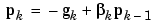
For the Polak-Ribiére update, the constant 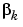is computed by

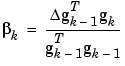
This is the inner product of the previous change in the gradient with the current gradient divided by the norm squared of the previous gradient. See [FlRe64] or [HDB96] for a discussion of the Polak-Ribiére conjugate gradient algorithm.

In the following code, we recreate our previous network and train it using the Polak-Ribiére version of the conjugate gradient algorithm. The training parameters for traincgp are the same as those for traincgf. The default line search routine srchcha is used in this example. The parameters show and epoch are set to the same values as they were for traincgf.

• p = [-1 -1 2 2;0 5 0 5];
  t = [-1 -1 1 1];
  net=newff(minmax(p),[3,1],{'tansig','purelin'},'traincgp');
  net.trainParam.show = 5;
  net.trainParam.epochs = 300;
  net.trainParam.goal = 1e-5;
  [net,tr]=train(net,p,t);
     TRAINCGP-srchcha, Epoch 0/300, MSE 1.21966/1e-05, Gradient 
  1.77008/1e-06
     TRAINCGP-srchcha, Epoch 5/300, MSE 0.227447/1e-05, Gradient 
  0.86507/1e-06
     TRAINCGP-srchcha, Epoch 10/300, MSE 0.000237395/1e-05, 
  Gradient 0.0174276/1e-06
     TRAINCGP-srchcha, Epoch 15/300, MSE 9.28243e-05/1e-05, 
  Gradient 0.00485746/1e-06
     TRAINCGP-srchcha, Epoch 20/300, MSE 1.46146e-05/1e-05, 
  Gradient 0.000912838/1e-06
     TRAINCGP-srchcha, Epoch 25/300, MSE 1.05893e-05/1e-05, 
  Gradient 0.00238173/1e-06
     TRAINCGP-srchcha, Epoch 26/300, MSE 9.10561e-06/1e-05, 
  Gradient 0.00197441/1e-06
     TRAINCGP, Performance goal met.
  a = sim(net,p)
  a =
     -0.9967   -1.0018    0.9958    1.0022
  

The traincgp routine has performance similar to traincgf. It is difficult to predict which algorithm will perform best on a given problem. The storage requirements for Polak-Ribiére (four vectors) are slightly larger than for Fletcher-Reeves (three vectors).

Powell-Beale Restarts (traincgb)

For all conjugate gradient algorithms, the search direction will be periodically reset to the negative of the gradient. The standard reset point occurs when the number of iterations is equal to the number of network parameters (weights and biases), but there are other reset methods that can improve the efficiency of training. One such reset method was proposed by Powell [Powe77], based on an earlier version proposed by Beale [Beal72]. For this technique we will restart if there is very little orthogonality left between the current gradient and the previous gradient. This is tested with the following inequality.

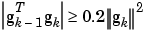
If this condition is satisfied, the search direction is reset to the negative of the gradient.

In the following code, we recreate our previous network and train it using the Powell-Beale version of the conjugate gradient algorithm. The training parameters for traincgb are the same as those for traincgf. The default line search routine srchcha is used in this example. The parameters show and epoch are set to the same values as they were for traincgf.

• p = [-1 -1 2 2;0 5 0 5];
  t = [-1 -1 1 1];
  net=newff(minmax(p),[3,1],{'tansig','purelin'},'traincgb');
  net.trainParam.show = 5;
  net.trainParam.epochs = 300;
  net.trainParam.goal = 1e-5;
  [net,tr]=train(net,p,t);
     TRAINCGB-srchcha, Epoch 0/300, MSE 2.5245/1e-05, Gradient 
  3.66882/1e-06
     TRAINCGB-srchcha, Epoch 5/300, MSE 4.86255e-07/1e-05, Gradient 
  0.00145878/1e-06
     TRAINCGB, Performance goal met.
  a = sim(net,p)
  a =
     -0.9997   -0.9998    1.0000    1.0014
  

The traincgb routine has performance that is somewhat better than traincgp for some problems, although performance on any given problem is difficult to predict. The storage requirements for the Powell-Beale algorithm (six vectors) are slightly larger than for Polak-Ribiére (four vectors).

Scaled Conjugate Gradient (trainscg)

Each of the conjugate gradient algorithms that we have discussed so far requires a line search at each iteration. This line search is computationally expensive, since it requires that the network response to all training inputs be computed several times for each search. The scaled conjugate gradient algorithm (SCG), developed by Moller [Moll93], was designed to avoid the time-consuming line search. This algorithm is too complex to explain in a few lines, but the basic idea is to combine the model-trust region approach (used in the Levenberg-Marquardt algorithm described later), with the conjugate gradient approach. See {Moll93] for a detailed explanation of the algorithm.

In the following code, we reinitialize our previous network and retrain it using the scaled conjugate gradient algorithm. The training parameters for trainscg are epochs, show, goal, time, min_grad, max_fail, sigma, lambda. We have previously discussed the first six parameters. The parameter sigma determines the change in the weight for the second derivative approximation. The parameter lambda regulates the indefiniteness of the Hessian. The parameters show and epoch are set to 10 and 300, respectively.

• p = [-1 -1 2 2;0 5 0 5];
  t = [-1 -1 1 1];
  net=newff(minmax(p),[3,1],{'tansig','purelin'},'trainscg');
  net.trainParam.show = 10;
  net.trainParam.epochs = 300;
  net.trainParam.goal = 1e-5;
  [net,tr]=train(net,p,t);
     TRAINSCG, Epoch 0/300, MSE 4.17697/1e-05, Gradient 
  5.32455/1e-06
     TRAINSCG, Epoch 10/300, MSE 2.09505e-05/1e-05, Gradient 
  0.00673703/1e-06
     TRAINSCG, Epoch 11/300, MSE 9.38923e-06/1e-05, Gradient 
  0.0049926/1e-06
     TRAINSCG, Performance goal met.
  a = sim(net,p)
  a =
     -1.0057   -1.0008    1.0019    1.0005
  

The trainscg routine may require more iterations to converge than the other conjugate gradient algorithms, but the number of computations in each iteration is significantly reduced because no line search is performed. The storage requirements for the scaled conjugate gradient algorithm are about the same as those of Fletcher-Reeves.

Resilient Backpropagation (trainrp)

Line Search Routines

© 1994-2005 The MathWorks, Inc.