Neural Network Toolbox

Using the NN Predictive Controller Block

This section demonstrates how the NN Predictive Controller block is used.The first step is to copy the NN Predictive Controller block from the Neural Network Toolbox blockset to your model window. See your Simulink documentation if you are not sure how to do this. This step is skipped in the following demonstration.

A demo model is provided with the Neural Network Toolbox to demonstrate the predictive controller. This demo uses a catalytic Continuous Stirred Tank Reactor (CSTR). A diagram of the process is shown in the following figure.

The dynamic model of the system is

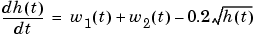
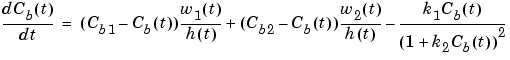
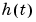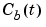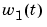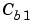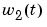where is the liquid level, is the product concentration at the output of the process, is the flow rate of the concentrated feed , and is the flow rate of the diluted feed 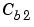. The input concentrations are set to 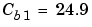and 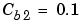. The constants associated with the rate of consumption are 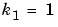and .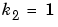

The objective of the controller is to maintain the product concentration by adjusting the flow 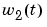. To simplify the demonstration, we set 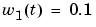. The level of the tank 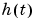is not controlled for this experiment.

To run this demo, follow these steps.

1. Start MATLAB®.
2. Run the demo model by typing predcstr in the MATLAB command window. This command starts Simulink and creates the following model window. The NN Predictive Controller block has already been placed in the model.

   

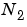3. Double-click the NN Predictive Controller block. This brings up the following window for designing the model predictive controller. This window enables you to change the controller horizons and 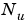. ( 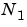is fixed at 1.) The weighting parameter 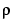, described earlier, is also defined in this window. The parameter 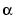is used to control the optimization. It determines how much reduction in performance is required for a successful optimization step. You can select which linear minimization routine is used by the optimization algorithm, and you can decide how many iterations of the optimization algorithm are performed at each sample time. The linear minimization routines are slight modifications of those discussed in Backpropagation.

   

4. Select Plant Identification. This opens the following window. The neural network plant model must be developed before the controller is used. The plant model predicts future plant outputs. The optimization algorithm uses these predictions to determine the control inputs that optimize future performance. The plant model neural network has one hidden layer, as shown earlier. The size of that layer, the number of delayed inputs and delayed outputs, and the training function are selected in this window. You can select any of the training functions described in Backpropagation, to train the neural network plant model.

   .
   
   

5. Select the Generate Training Data button. The program generates training data by applying a series of random step inputs to the Simulink plant model. The potential training data is then displayed in a figure similar to the following.

   

6. Select Accept Data, and then select Train Network from the Plant Identification window. Plant model training begins. The training proceeds according to the selected training algorithm (trainlm in this case). This is a straightforward application of batch training, as described in Backpropagation. After the training is complete, the response of the resulting plant model is displayed, as in the following figure. (There are also separate plots for validation and testing data, if they exist.) You can then continue training with the same data set by selecting Train Network again, you can Erase Generated Data and generate a new data set, or you can accept the current plant model and begin simulating the closed loop system. For this demonstration, begin the simulation, as shown in the following steps.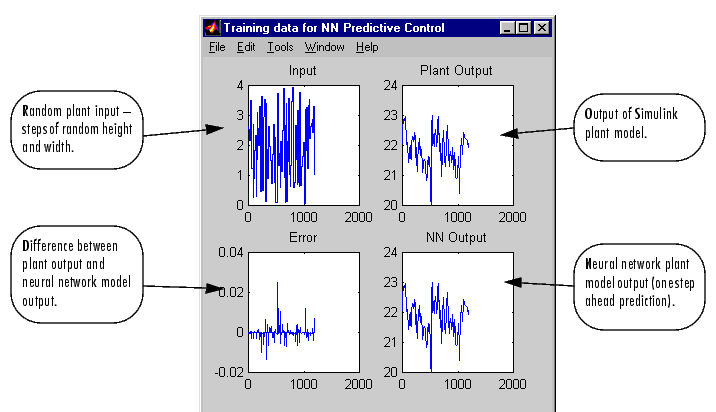
   
   
7. Select OK in the Plant Identification window. This loads the trained neural network plant model into the NN Predictive Controller block.
8. Select OK in the Neural Network Predictive Control window. This loads the controller parameters into the NN Predictive Controller block.
9. Return to the Simulink model and start the simulation by choosing the Start command from the Simulation menu. As the simulation runs, the plant output and the reference signal are displayed, as in the following figure.

   

Predictive Control

NARMA-L2 (Feedback Linearization) Control

© 1994-2005 The MathWorks, Inc.