Identification of the NARMA-L2 Model :: Control Systems (Neural Network Toolbox)

Neural Network Toolbox

Identification of the NARMA-L2 Model

As with the model predictive control, the first step in using feedback linearization (or NARMA-L2 control) is to identify the system to be controlled. You train a neural network to represent the forward dynamics of the system. The first step is to choose a model structure to use. One standard model that has been used to represent general discrete-time nonlinear systems is the Nonlinear Autoregressive-Moving Average (NARMA) model:

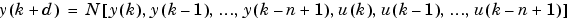
where 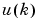is the system input, and 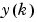is the system output. For the identification phase, you could train a neural network to approximate the nonlinear function . This is the identification procedure used for the NN Predictive Controller.

If you want the system output to follow some reference trajectory, 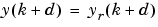, the next step is to develop a nonlinear controller of the form:

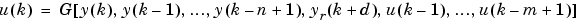
The problem with using this controller is that if you want to train a neural network to create the function 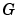that will minimize mean square error, you need to use dynamic backpropagation ([NaPa91] or [HaJe99]). This can be quite slow. One solution proposed by Narendra and Mukhopadhyay [NaMu97] is to use approximate models to represent the system. The controller used in this section is based on the NARMA-L2 approximate model:

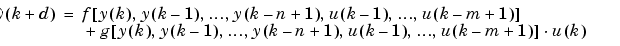
This model is in companion form, where the next controller input 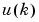is not contained inside the nonlinearity. The advantage of this form is that you can solve for the control input that causes the system output to follow the reference 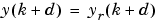. The resulting controller would have the form

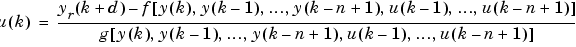
Using this equation directly can cause realization problems, because you must determine the control input 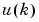based on the output at the same time, 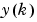. So, instead, use the model

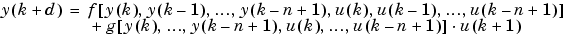
where 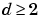. The following figure shows the structure of a neural network representation.

NARMA-L2 (Feedback Linearization) Control NARMA-L2 Controller