

| Neural Network Toolbox |   |
Creating a Linear Neuron (newlin)
Consider a single linear neuron with two inputs. The diagram for this network is shown below.
The weight matrix W in this case has only one row. The network output is:
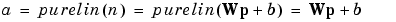 or
or
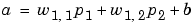
Like the perceptron, the linear network has a decision boundary that is determined by the input vectors for which the net input n is zero. For 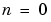 the equation
the equation 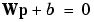 specifies such a decision boundary as shown below (adapted with thanks from [HDB96]).
specifies such a decision boundary as shown below (adapted with thanks from [HDB96]).
Input vectors in the upper right gray area will lead to an output greater than 0. Input vectors in the lower left white area will lead to an output less than 0. Thus, the linear network can be used to classify objects into two categories. However, it can classify in this way only if the objects are linearly separable. Thus, the linear network has the same limitation as the perceptron.
We can create a network like that shown above with the command
The first matrix of arguments specifies the range of the two scalar inputs. The last argument, 1, says that the network has a single output.
The network weights and biases are set to zero by default. You can see the current values with the commands
However, you can give the weights any value that you want, such as 2 and 3 respectively, with
The bias can be set and checked in the same way.
You can simulate the linear network for a particular input vector. Try
Now you can find the network output with the function sim.
To summarize, you can create a linear network with newlin, adjust its elements as you want, and simulate it with sim. You can find more about newlin by typing help newlin.
 | Network Architecture | Mean Square Error |  |
© 1994-2005 The MathWorks, Inc.