| Neural Network Toolbox | |
Network Architectures
Two or more of the neurons shown earlier can be combined in a layer, and a particular network could contain one or more such layers. First consider a single layer of neurons.
A Layer of Neurons
A one-layer network with R input elements and S neurons follows.
In this network, each element of the input vector p is connected to each neuron input through the weight matrix W. The ith neuron has a summer that gathers its weighted inputs and bias to form its own scalar output n(i). The various n(i) taken together form an S-element net input vector n. Finally, the neuron layer outputs form a column vector a. We show the expression for a at the bottom of the figure.
Note that it is common for the number of inputs to a layer to be different from the number of neurons (i.e., R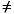 
S). A layer is not constrained to have the number of its inputs equal to the number of its neurons.
You can create a single (composite) layer of neurons having different transfer functions simply by putting two of the networks shown earlier in parallel. Both networks would have the same inputs, and each network would create some of the outputs.
The input vector elements enter the network through the weight matrix W.
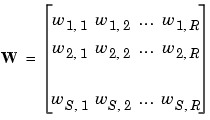
Note that the row indices on the elements of matrix W indicate the destination neuron of the weight, and the column indices indicate which source is the input for that weight. Thus, the indices in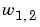 
say that the strength of the signal from the second input element to the first (and only) neuron is
.
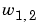The S neuron R input one-layer network also can be drawn in abbreviated notation.
Here p is an R length input vector, W is an SxR matrix, and a and b are S length vectors. As defined previously, the neuron layer includes the weight matrix, the multiplication operations, the bias vector b, the summer, and the transfer function boxes.
Inputs and Layers
We are about to discuss networks having multiple layers so we will need to extend our notation to talk about such networks. Specifically, we need to make a distinction between weight matrices that are connected to inputs and weight matrices that are connected between layers. We also need to identify the source and destination for the weight matrices.
We will call weight matrices connected to inputs, input weights; and we will call weight matrices coming from layer outputs, layer weights. Further, we will use superscripts to identify the source (second index) and the destination (first index) for the various weights and other elements of the network. To illustrate, we have taken the one-layer multiple input network shown earlier and redrawn it in abbreviated form below.
As you can see, we have labeled the weight matrix connected to the input vector p as an Input Weight matrix (IW1,1) having a source 1 (second index) and a destination 1 (first index). Also, elements of layer one, such as its bias, net input, and output have a superscript 1 to say that they are associated with the first layer.
In the next section, we will use Layer Weight (LW) matrices as well as Input Weight (IW) matrices.
You might recall from the notation section of the Preface that conversion of the layer weight matrix from math to code for a particular network called net is:
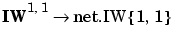
Thus, we could write the code to obtain the net input to the transfer function as:
| | Neuron with Vector Input | Multiple Layers of Neurons | |
© 1994-2005 The MathWorks, Inc.
