

| Neural Network Toolbox |   |
Self-Organizing Maps
Self-organizing feature maps (SOFM) learn to classify input vectors according to how they are grouped in the input space. They differ from competitive layers in that neighboring neurons in the self-organizing map learn to recognize neighboring sections of the input space. Thus, self-organizing maps learn both the distribution (as do competitive layers) and topology of the input vectors they are trained on.
The neurons in the layer of an SOFM are arranged originally in physical positions according to a topology function. The functions gridtop, hextop or randtop can arrange the neurons in a grid, hexagonal, or random topology. Distances between neurons are calculated from their positions with a distance function. There are four distance functions, dist, boxdist, linkdist and mandist. Link distance is the most common. These topology and distance functions are described in detail later in this section.
Here a self-organizing feature map network identifies a winning neuron 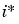 using the same procedure as employed by a competitive layer. However, instead of updating only the winning neuron, all neurons within a certain neighborhood
using the same procedure as employed by a competitive layer. However, instead of updating only the winning neuron, all neurons within a certain neighborhood 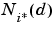 of the winning neuron are updated using the Kohonen rule. Specifically, we adjust all such neurons
of the winning neuron are updated using the Kohonen rule. Specifically, we adjust all such neurons 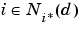 as follows.
as follows.
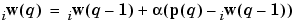 or
or
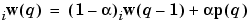
Here the neighborhood 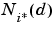 contains the indices for all of the neurons that lie within a radius
contains the indices for all of the neurons that lie within a radius 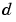 of the winning neuron
of the winning neuron 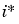 .
.
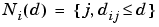
Thus, when a vector 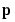 is presented, the weights of the winning neuron and its close neighbors move toward
is presented, the weights of the winning neuron and its close neighbors move toward 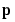 . Consequently, after many presentations, neighboring neurons will have learned vectors similar to each other.
. Consequently, after many presentations, neighboring neurons will have learned vectors similar to each other.
To illustrate the concept of neighborhoods, consider the figure given below. The left diagram shows a two-dimensional neighborhood of radius 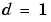 around neuron
around neuron 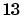 . The right diagram shows a neighborhood of radius
. The right diagram shows a neighborhood of radius 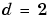 .
.
These neighborhoods could be written as
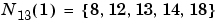 and
and
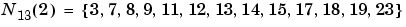
Note that the neurons in an SOFM do not have to be arranged in a two-dimensional pattern. You can use a one-dimensional arrangement, or even three or more dimensions. For a one-dimensional SOFM, a neuron has only two neighbors within a radius of 1 (or a single neighbor if the neuron is at the end of the line).You can also define distance in different ways, for instance, by using rectangular and hexagonal arrangements of neurons and neighborhoods. The performance of the network is not sensitive to the exact shape of the neighborhoods.
 | Graphical Example | Topologies (gridtop, hextop, randtop) |  |
© 1994-2005 The MathWorks, Inc.