| Neural Network Toolbox | |
Competitive Learning
The neurons in a competitive layer distribute themselves to recognize frequently presented input vectors.
Architecture
The architecture for a competitive network is shown below.
The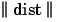 
box in this figure accepts the input vector p and the input weight matrix IW1,1, and produces a vector having S1 elements. The elements are the negative of the distances between the input vector and vectors iIW1,1 formed from the rows of the input weight matrix.
The net input n1 of a competitive layer is computed by finding the negative distance between input vector p and the weight vectors and adding the biases b. If all biases are zero, the maximum net input a neuron can have is 0. This occurs when the input vector p equals that neuron's weight vector.
The competitive transfer function accepts a net input vector for a layer and returns neuron outputs of 0 for all neurons except for the winner, the neuron associated with the most positive element of net input n1. The winner's output is 1. If all biases are 0, then the neuron whose weight vector is closest to the input vector has the least negative net input and, therefore, wins the competition to output a 1.
Reasons for using biases with competitive layers are introduced in a later section on training.
| | Important Self-Organizing and LVQ Functions | Creating a Competitive Neural Network (newc) | |
© 1994-2005 The MathWorks, Inc.
