Signal Processing Toolbox

Filter Implementation and Analysis

This section describes how to filter discrete signals using the MATLAB filter function and other functions in the Signal Processing Toolbox. It also discusses how to use the toolbox functions to analyze filter characteristics, including impulse response, magnitude and phase response, group delay, and zero-pole locations.

Convolution and Filtering

The mathematical foundation of filtering is convolution. The MATLAB conv function performs standard one-dimensional convolution, convolving one vector with another:

• conv([1 1 1],[1 1 1])
  ans =
       1     2     3     2     1
  

Note    Convolve rectangular matrices for two-dimensional signal processing using the conv2 function.

A digital filter's output y(k) is related to its input x(k) by convolution with its impulse response h(k).

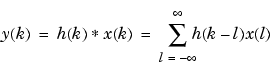
If a digital filter's impulse response h(k) is finite length, and the input x(k) is also finite length, you can implement the filter using conv. Store x(k) in a vector x, h(k) in a vector h, and convolve the two:

• x = randn(5,1);   % A random vector of length 5
  h = [1 1 1 1]/4;  % Length 4 averaging filter
  y = conv(h,x);
  

Working with Data

Filters and Transfer Functions

© 1994-2005 The MathWorks, Inc.