Signal Processing Toolbox

Filtering with the filter Function

It is simple to work back to a difference equation from the z-transform relation shown earlier. Assume that a(1) = 1. Move the denominator to the left-hand side and take the inverse z-transform.

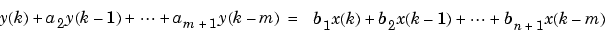
In terms of current and past inputs, and past outputs, y(n) is

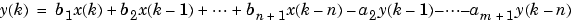
This is the standard time-domain representation of a digital filter, computed starting with y(1) and assuming zero initial conditions. This representation's progression is

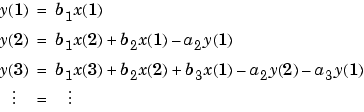
A filter in this form is easy to implement with the filter function. For example, a simple single-pole filter (lowpass) is

• b = 1;          % Numerator
  a = [1 -0.9];   % Denominator
  

where the vectors b and a represent the coefficients of a filter in transfer function form. To apply this filter to your data, use

• y = filter(b,a,x);
  

filter gives you as many output samples as there are input samples, that is, the length of y is the same as the length of x. If the first element of a is not 1, filter divides the coefficients by a(1) before implementing the difference equation.

Filters and Transfer Functions

The filter Function

© 1994-2005 The MathWorks, Inc.