

| Signal Processing Toolbox |   |
Continuous-Time System Models
The continuous-time system models are representational schemes for analog filters. Many of the discrete-time system models described earlier are also appropriate for the representation of continuous-time systems:
It is possible to represent any system of linear time-invariant differential equations as a set of first-order differential equations. In matrix or state-space form, you can express the equations as
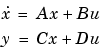
where u is a vector of nu inputs, x is an nx-element state vector, and y is a vector of ny outputs. In MATLAB, store A, B, C, and D in separate rectangular arrays.
An equivalent representation of the state-space system is the Laplace transform transfer function description
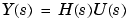
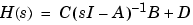
For single-input, single-output systems, this form is given by
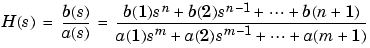
Given the coefficients of a Laplace transform transfer function, residue determines the partial fraction expansion of the system. See the description of residue in the MATLAB documentation for details.
The factored zero-pole-gain form is
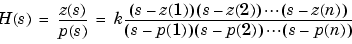
As in the discrete-time case, MATLAB stores polynomial coefficients in row vectors in descending powers of s. MATLAB stores polynomial roots, or zeros and poles, in column vectors.
 | Linear System Models | Linear System Transformations |  |
© 1994-2005 The MathWorks, Inc.