buffer (Signal Processing Toolbox)

Buffer signal vector into matrix of data frames

Syntax

y = buffer(x,n)
y = buffer(x,n,p)
y = buffer(x,n,p,opt)
[y,z] = buffer(...)
[y,z,opt] = buffer(...)

Description

y = buffer(x,n) partitions a length-L signal vector x into nonoverlapping data segments (frames) of length n. Each data frame occupies one column of matrix output y, which has n rows and ceil(L/n) columns. If L is not evenly divisible by n, the last column is zero-padded to length n.

y = buffer(x,n,p) overlaps or underlaps successive frames in the output matrix by p samples:

For 0 < p < n (overlap), buffer repeats the final p samples of each frame at the beginning of the following frame. For example, if x = 1:30 and n = 7, an overlap of p = 3 looks like this.

The first frame starts with p zeros (the default initial condition), and the number of columns in y is ceil(L/(n-p)).

For p < 0 (underlap), buffer skips p samples between consecutive frames. For example, if x = 1:30 and n = 7, a buffer with underlap of p = -3 looks like this.

The number of columns in y is ceil(L/(n-p)).

y = buffer(x,n,p,opt) specifies a vector of samples to precede x(1) in an overlapping buffer, or the number of initial samples to skip in an underlapping buffer:

For 0 < p < n (overlap), opt specifies a length-p vector to insert before x(1) in the buffer. This vector can be considered an initial condition, which is needed when the current buffering operation is one in a sequence of consecutive buffering operations. To maintain the desired frame overlap from one buffer to the next, opt should contain the final p samples of the previous buffer in the sequence. See "Continuous Buffering" below.

By default, opt is zeros(p,1) for an overlapping buffer. Set opt to 'nodelay' to skip the initial condition and begin filling the buffer immediately with x(1). In this case, L must be length(p) or longer. For example, if x = 1:30 and n = 7, a buffer with overlap of p = 3 looks like this.

For p < 0 (underlap), opt is an integer value in the range [0,-p] specifying the number of initial input samples, x(1:opt), to skip before adding samples to the buffer. The first value in the buffer is therefore x(opt+1). By default, opt is zero for an underlapping buffer.

This option is especially useful when the current buffering operation is one in a sequence of consecutive buffering operations. To maintain the desired frame underlap from one buffer to the next, opt should equal the difference between the total number of points to skip between frames (p) and the number of points that were available to be skipped in the previous input to buffer. If the previous input had fewer than p points that could be skipped after filling the final frame of that buffer, the remaining opt points need to be removed from the first frame of the current buffer. See "Continuous Buffering" below for an example of how this works in practice.

[y,z] = buffer(...) partitions the length-L signal vector x into frames of length n, and outputs only the full frames in y. If y is an overlapping buffer, it has n rows and m columns, where

m = floor(L/(n-p))      % When length(opt) = p

m = floor((L-n)/(n-p))+1% When opt = 'nodelay'

If y is an underlapping buffer, it has n rows and m columns, where

m = floor((L-opt)/(n-p)) + (rem((L-opt),(n-p)) >= n)

If the number of samples in the input vector (after the appropriate overlapping or underlapping operations) exceeds the number of places available in the n-by-m buffer, the remaining samples in x are output in vector z, which for an overlapping buffer has length

length(z) = L - m*(n-p) % When length(opt) = p

length(z) = L - ((m-1)*(n-p)+n)% When opt = 'nodelay'

and for an underlapping buffer has length

```
length(z) = (L-opt) - m*(n-p)
```

Output z shares the same orientation (row or column) as x. If there are no remaining samples in the input after the buffer with the specified overlap or underlap is filled, z is an empty vector.

[y,z,opt] = buffer(...) returns the last p samples of a overlapping buffer in output opt. In an underlapping buffer, opt is the difference between the total number of points to skip between frames (-p) and the number of points in x that were available to be skipped after filling the last frame:

For 0 < p < n (overlap), opt (as an output) contains the final p samples in the last frame of the buffer. This vector can be used as the initial condition for a subsequent buffering operation in a sequence of consecutive buffering operations. This allows the desired frame overlap to be maintained from one buffer to the next. See "Continuous Buffering" below.
For p < 0 (underlap), opt (as an output) is the difference between the total number of points to skip between frames (-p) and the number of points in x that were available to be skipped after filling the last frame.

opt = m*(n-p) + opt - L     % z is the empty vector.

where opt on the right-hand side is the input argument to buffer, and opt on the left-hand side is the output argument. Here m is the number of columns in the buffer, which is
- ```
m = floor((L-opt)/(n-p)) + (rem((L-opt),(n-p))>=n)
```
Note that for an underlapping buffer output opt is always zero when output z contains data.

The opt output for an underlapping buffer is especially useful when the current buffering operation is one in a sequence of consecutive buffering operations. The opt output from each buffering operation specifies the number of samples that need to be skipped at the start of the next buffering operation to maintain the desired frame underlap from one buffer to the next. If fewer than p points were available to be skipped after filling the final frame of the current buffer, the remaining opt points need to be removed from the first frame of the next buffer.

In a sequence of buffering operations, the opt output from each operation should be used as the opt input to the subsequent buffering operation. This ensures that the desired frame overlap or underlap is maintained from buffer to buffer, as well as from frame to frame within the same buffer. See "Continuous Buffering" below for an example of how this works in practice.

Continuous Buffering

In a continuous buffering operation, the vector input to the buffer function represents one frame in a sequence of frames that make up a discrete signal. These signal frames can originate in a frame-based data acquisition process, or within a frame-based algorithm like the FFT.

As an example, you might acquire data from an A/D card in frames of 64 samples. In the simplest case, you could rebuffer the data into frames of 16 samples; buffer with n = 16 creates a buffer of four frames from each 64-element input frame. The result is that the signal of frame size 64 has been converted to a signal of frame size 16; no samples were added or removed.

In the general case where the original signal frame size, L, is not equally divisible by the new frame size, n, the overflow from the last frame needs to be captured and recycled into the following buffer. You can do this by iteratively calling buffer on input x with the two-output-argument syntax:

[y,z] = buffer([z;x],n)     % x is a column vector.
[y,z] = buffer([z,x],n)     % x is a row vector.

This simply captures any buffer overflow in z, and prepends the data to the subsequent input in the next call to buffer. Again, the input signal, x, of frame size L, has been converted to a signal of frame size n without any insertion or deletion of samples.

Note that continuous buffering cannot be done with the single-output syntax y = buffer(...), because the last frame of y in this case is zero padded, which adds new samples to the signal.

Continuous buffering in the presence of overlap and underlap is handled with the opt parameter, which is used as both an input and output to buffer. The following two examples demonstrate how the opt parameter should be used.

Examples

Example 1: Continuous Overlapping Buffers

First create a buffer containing 100 frames, each with 11 samples:

data = buffer(1:1100,11);% 11 samples per frame

Imagine that the frames (columns) in the matrix called data are the sequential outputs of a data acquisition board sampling a physical signal: data(:,1) is the first D/A output, containing the first 11 signal samples; data(:,2) is the second output, containing the next 11 signal samples, and so on.

You want to rebuffer this signal from the acquired frame size of 11 to a frame size of 4 with an overlap of 1. To do this, you will repeatedly call buffer to operate on each successive input frame, using the opt parameter to maintain consistency in the overlap from one buffer to the next.

Set the buffer parameters:

n = 4; % New frame size
p = 1; % Overlap
opt = -5;% Value of y(1)
z = [];% Initialize the carry-over vector.

Now repeatedly call buffer, each time passing in a new signal frame from data. Note that overflow samples (returned in z) are carried over and prepended to the input in the subsequent call to buffer:

for i=1:size(data,2),    % Loop over each source frame (column).
   x = data(:,i);% A single frame of the D/A output
   [y,z,opt] = buffer([z;x],n,p,opt);
   disp(y);% Display the buffer of data.
   pause
end

Here's what happens during the first four iterations.

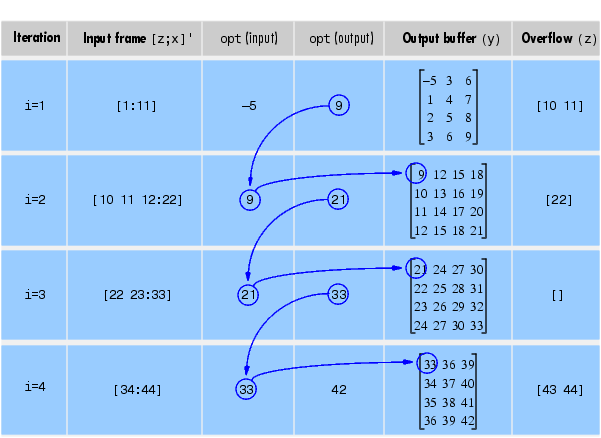
Note that the size of the output matrix, y, can vary by a single column from one iteration to the next. This is typical for buffering operations with overlap or underlap.

Example 2: Continuous Underlapping Buffers

Again create a buffer containing 100 frames, each with 11 samples:

data = buffer(1:1100,11); % 11 samples per frame

Again, imagine that data(:,1) is the first D/A output, containing the first 11 signal samples; data(:,2) is the second output, containing the next 11 signal samples, and so on.

You want to rebuffer this signal from the acquired frame size of 11 to a frame size of 4 with an underlap of 2. To do this, you will repeatedly call buffer to operate on each successive input frame, using the opt parameter to maintain consistency in the underlap from one buffer to the next.

Set the buffer parameters:

n = 4;     % New frame size
p = -2;    % Underlap
opt = 1;   % Skip the first input element, x(1).
z = [];    % Initialize the carry-over vector.

for i=1:size(data,2),     % Loop over each source frame (column).
   x = data(:,i);         % A single frame of the D/A output
   [y,z,opt] = buffer([z;x],n,p,opt);
   disp(y);       % Display the buffer of data.
   pause
end

Here's what happens during the first three iterations.

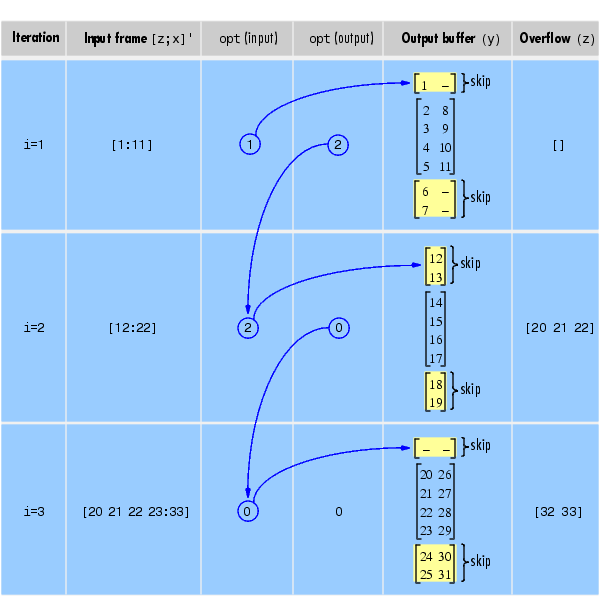
Diagnostics

Error messages are displayed when p 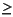n or length(opt)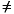length(p) in an overlapping buffer case:

Frame overlap P must be less than the buffer size N.
Initial conditions must be specified as a length-P vector.

See Also

reshape

bohmanwin buttap