Filter Requirements and Specification :: Filter Design and Implementation (Signal Processing Toolbox)

Signal Processing Toolbox

Filter Requirements and Specification

The goal of filter design is to perform frequency dependent alteration of a data sequence. A possible requirement might be to remove noise above 30 Hz from a data sequence sampled at 100 Hz. A more rigorous specification might call for a specific amount of passband ripple, stopband attenuation, or transition width. A very precise specification could ask to achieve the performance goals with the minimum filter order, or it could call for an arbitrary magnitude shape, or it might require an FIR filter.

Filter design methods differ primarily in how performance is specified. For "loosely specified" requirements, as in the first case above, a Butterworth IIR filter is often sufficient. To design a fifth-order 30 Hz lowpass Butterworth filter and apply it to the data in vector x:

[b,a] = butter(5,30/50);
Hd = dfilt.df2t(b,a);        %Direct-form II transposed structure
y = filter(Hd,x);

The second input argument to butter specifies the cutoff frequency, normalized to half the sampling frequency (the Nyquist frequency).

All of the filter design functions operate with normalized frequencies, so they do not require the system sampling rate as an extra input argument. This toolbox uses the convention that unit frequency is the Nyquist frequency, defined as half the sampling frequency. The normalized frequency, therefore, is always in the interval 0 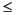f 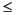1. For a system with a 1000 Hz sampling frequency, 300 Hz is 300/500 = 0.6. To convert normalized frequency to angular frequency around the unit circle, multiply by 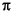. To convert normalized frequency back to hertz, multiply by half the sample frequency.

More rigorous filter requirements traditionally include passband ripple (Rp, in decibels), stopband attenuation (Rs, in decibels), and transition width (Ws-Wp, in hertz).

You can design Butterworth, Chebyshev Type I, Chebyshev Type II, and elliptic filters that meet this type of performance specification. The toolbox order selection functions estimate the minimum filter order that meets a given set of requirements.

To meet specifications with more rigid constraints like linear phase or arbitrary filter shape, use the FIR and direct IIR filter design routines.

Filter Design and Implementation IIR Filter Design