Comparison of Classical IIR Filter Types :: Filter Design and Implementation (Signal Processing Toolbox)

Signal Processing Toolbox

Comparison of Classical IIR Filter Types

The toolbox provides five different types of classical IIR filters, each optimal in some way. This section shows the basic analog prototype form for each and summarizes major characteristics.

Butterworth Filter

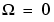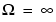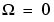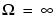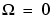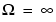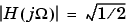The Butterworth filter provides the best Taylor Series approximation to the ideal lowpass filter response at analog frequencies and ; for any order N, the magnitude squared response has 2N-1 zero derivatives at these locations (maximally flat at and ). Response is monotonic overall, decreasing smoothly from to . at .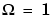

Chebyshev Type I Filter

The Chebyshev Type I filter minimizes the absolute difference between the ideal and actual frequency response over the entire passband by incorporating an equal ripple of Rp dB in the passband. Stopband response is maximally flat. The transition from passband to stopband is more rapid than for the Butterworth filter. at .

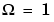Chebyshev Type II Filter

The Chebyshev Type II filter minimizes the absolute difference between the ideal and actual frequency response over the entire stopband by incorporating an equal ripple of Rs dB in the stopband. Passband response is maximally flat.

The stopband does not approach zero as quickly as the type I filter (and does not approach zero at all for even-valued filter order n). The absence of ripple in the passband, however, is often an important advantage. 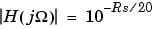at .

Elliptic Filter

Elliptic filters are equiripple in both the passband and stopband. They generally meet filter requirements with the lowest order of any supported filter type. Given a filter order n, passband ripple Rp in decibels, and stopband ripple Rs in decibels, elliptic filters minimize transition width. 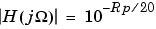at .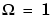

Bessel Filter

Analog Bessel lowpass filters have maximally flat group delay at zero frequency and retain nearly constant group delay across the entire passband. Filtered signals therefore maintain their waveshapes in the passband frequency range. Frequency mapped and digital Bessel filters, however, do not have this maximally flat property; this toolbox supports only the analog case for the complete Bessel filter design function.

Bessel filters generally require a higher filter order than other filters for satisfactory stopband attenuation. 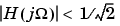at 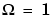and decreases as filter order n increases.

Note The lowpass filters shown above were created with the analog prototype functions besselap, buttap, cheb1ap, cheb2ap, and ellipap. These functions find the zeros, poles, and gain of an order n analog filter of the appropriate type with cutoff frequency of 1 rad/s. The complete filter design functions (besself, butter, cheby1, cheby2, and ellip) call the prototyping functions as a first step in the design process. See "Special Topics in IIR Filter Design" for details.

To create similar plots, use n = 5 and, as needed, Rp = 0.5 and Rs = 20. For example, to create the elliptic filter plot:

[z,p,k] = ellipap(5,0.5,20);
w = logspace(-1,1,1000);
h = freqs(k*poly(z),poly(p),w);
semilogx(w,abs(h)), grid

Direct IIR Filter Design

This toolbox uses the term direct methods to describe techniques for IIR design that find a filter based on specifications in the discrete domain. Unlike the analog prototyping method, direct design methods are not constrained to the standard lowpass, highpass, bandpass, or bandstop configurations. Rather, these functions design filters with an arbitrary, perhaps multiband, frequency response. This section discusses the yulewalk function, which is intended specifically for filter design; Parametric Modeling discusses other methods that may also be considered direct, such as Prony's method, Linear Prediction, the Steiglitz-McBride method, and inverse frequency design.

The yulewalk function designs recursive IIR digital filters by fitting a specified frequency response. yulewalk's name reflects its method for finding the filter's denominator coefficients: it finds the inverse FFT of the ideal desired power spectrum and solves the "modified Yule-Walker equations" using the resulting autocorrelation function samples. The statement

```
[b,a] = yulewalk(n,f,m)
```

returns row vectors b and a containing the n+1 numerator and denominator coefficients of the order n IIR filter whose frequency-magnitude characteristics approximate those given in vectors f and m. f is a vector of frequency points ranging from 0 to 1, where 1 represents the Nyquist frequency. m is a vector containing the desired magnitude response at the points in f. f and m can describe any piecewise linear shape magnitude response, including a multiband response. The FIR counterpart of this function is fir2, which also designs a filter based on an arbitrary piecewise linear magnitude response. See "FIR Filter Design" for details.

Note that yulewalk does not accept phase information, and no statements are made about the optimality of the resulting filter.

Design a multiband filter with yulewalk, and plot the desired and actual frequency response:

m = [0   0   1   1   0   0   1   1   0 0];
f = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1];
[b,a] = yulewalk(10,f,m);
[h,w] = freqz(b,a,128)
plot(f,m,w/pi,abs(h))

Generalized Butterworth Filter Design

The toolbox function maxflat enables you to design generalized Butterworth filters, that is, Butterworth filters with differing numbers of zeros and poles. This is desirable in some implementations where poles are more expensive computationally than zeros. maxflat is just like the butter function, except that it you can specify two orders (one for the numerator and one for the denominator) instead of just one. These filters are maximally flat. This means that the resulting filter is optimal for any numerator and denominator orders, with the maximum number of derivatives at 0 and the Nyquist frequency = 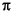both set to 0.

For example, when the two orders are the same, maxflat is the same as butter:

[b,a] = maxflat(3,3,0.25)
b =
    0.0317    0.0951    0.0951    0.0317
a =
    1.0000   -1.4590    0.9104   -0.1978
[b,a] = butter(3,0.25)
b =
    0.0317    0.0951    0.0951    0.0317
a =
    1.0000   -1.4590    0.9104   -0.1978

However, maxflat is more versatile because it allows you to design a filter with more zeros than poles:

[b,a] = maxflat(3,1,0.25)
b =
    0.0950    0.2849    0.2849    0.0950
a =
    1.0000   -0.2402

The third input to maxflat is the half-power frequency, a frequency between 0 and 1 with a desired magnitude response of .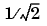

You can also design linear phase filters that have the maximally flat property using the 'sym' option:

maxflat(4,'sym',0.3)
ans =
    0.0331    0.2500    0.4337    0.2500    0.0331

For complete details of the maxflat algorithm, see Selesnick and Burrus [2].

Classical IIR Filter Design Using Analog Prototyping FIR Filter Design