filternorm (Signal Processing Toolbox)

Signal Processing Toolbox

filternorm

2-norm or infinity-norm of a digital filter

Syntax

```
filternorm(b,a)
filternorm(b,a,pnorm)
```

filternorm(b,a,2,tol)

Description

A typical use for filter norms is in digital filter scaling to reduce quantization effects. Scaling often improves the signal-to-noise ratio of the filter without resulting in data overflow. You, also, can use the 2-norm to compute the energy of the impulse response of a filter.

filternorm(b,a) computes the 2-norm of the digital filter defined by the numerator coefficients in b and denominator coefficients in a.

filternorm(b,a,pnorm) computes the 2- or infinity-norm (inf-norm) of the digital filter, where pnorm is either 2 or inf.

filternorm(b,a,2,tol) computes the 2-norm of an IIR filter with the specified tolerance, tol. The tolerance can be specified only for IIR 2-norm computations. pnorm in this case must be 2. If tol is not specified, it defaults to 1e-8.

Examples

Compute the 2-norm with a tolerance of 1e-10 of an IIR filter:

[b,a]=butter(5,.5);
L2=filternorm(b,a,2,1e-10)

L2 =

    0.7071

Compute the inf-norm of an FIR filter:

b=firpm(30,[.1 .9],[1 1],'Hilbert');
Linf=filternorm(b,1,inf)

Linf =

    1.0028

Algorithm

Given a filter H(z) with frequency reponse H(e^j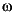), the L_p-norm is given by

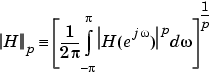
For the cas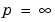e , the 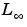norm simplifies to

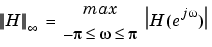
For the case p = 2, Parseval's theorem states that

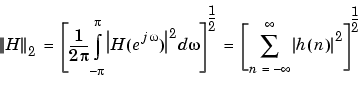
where h(n) is the impulse response of the filter. The energy of the impulse response, then, is .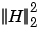

See Also

zp2sos, norm

Reference

Jackson, L.B., Digital Filters and Signal Processing, Third Edition, Kluwer Academic Publishers, 1996, Chapter 11.

filter2 filtfilt