latcfilt (Signal Processing Toolbox)

Lattice and lattice-ladder filter implementation

Syntax

[f,g] = latcfilt(k,x)
[f,g] = latcfilt(k,v,x)
[f,g] = latcfilt(k,1,x)
[f,g,zf] = latcfilt(...,'ic',zi)

Description

When filtering data, lattice coefficients can be used to represent

FIR filters
All-pole IIR filters
Allpass IIR filters
General IIR filters

[f,g] = latcfilt(k,x) filters x with the FIR lattice coefficients in the vector k. f is the forward lattice filter result and g is the backward filter result. If 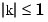, f corresponds to the minimum-phase output, and g corresponds to the maximum-phase output.

If k and x are vectors, the result is a (signal) vector. Matrix arguments are permitted under the following rules:

If x is a matrix and k is a vector, each column of x is processed through the lattice filter specified by k.
If x is a vector and k is a matrix, each column of k is used to filter x, and a signal matrix is returned.
If x and k are both matrices with the same number of columns, then the ith column of k is used to filter the ith column of x. A signal matrix is returned.

[f,g] = latcfilt(k,v,x) filters x with the IIR lattice coefficients k and ladder coefficients v. k and v must be vectors, while x can be a signal matrix.

[f,g] = latcfilt(k,1,x) filters x with the IIR lattice specified by k, where k and x can be vectors or matrices. f is the all-pole lattice filter result and g is the allpass filter result.

[f,g,zf] = latcfilt(...,'ic',zi) accepts a length-k vector zi specifying the initial condition of the lattice states. Output zf is a length-k vector specifying the final condition of the lattice states.

See Also

filter, latc2tf, tf2latc

latc2tf levinson