Cepstrum Analysis :: Special Topics (Signal Processing Toolbox)

Signal Processing Toolbox

Cepstrum Analysis

Cepstrum analysis is a nonlinear signal processing technique with a variety of applications in areas such as speech and image processing. The Signal Processing Toolbox provides three functions for cepstrum analysis.

Operation
Function

Complex cepstrum
cceps

Inverse complex cepstrum
icceps

Real cepstrum
rceps

Operation	Function
Complex cepstrum	`cceps`
Inverse complex cepstrum	`icceps`
Real cepstrum	`rceps`

The complex cepstrum for a sequence x is calculated by finding the complex natural logarithm of the Fourier transform of x, then the inverse Fourier transform of the resulting sequence.

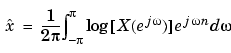
The toolbox function cceps performs this operation, estimating the complex cepstrum for an input sequence. It returns a real sequence the same size as the input sequence:

```
xhat = cceps(x)
```

For sequences that have roots on the unit circle, cepstrum analysis has numerical problems. See Oppenheim and Schafer [2] for information.

The complex cepstrum transformation is central to the theory and application of homomorphic systems, that is, systems that obey certain general rules of superposition. See Oppenheim and Schafer [3] for a discussion of the complex cepstrum and homomorphic transformations, with details on speech processing applications.

Try using cceps in an echo detection application. First, create a 45 Hz sine wave sampled at 100 Hz:

```
t = 0:0.01:1.27;
s1 = sin(2*pi*45*t);
```

Add an echo of the signal, with half the amplitude, 0.2 seconds after the beginning of the signal.

```
s2 = s1 + 0.5*[zeros(1,20) s1(1:108)];
```

The complex cepstrum of this new signal is

```
c = cceps(s2);
plot(t,c)
```

Note that the complex cepstrum shows a peak at 0.2 seconds, indicating the echo.

The real cepstrum of a signal x, sometimes called simply the cepstrum, is calculated by determining the natural logarithm of magnitude of the Fourier transform of x, then obtaining the inverse Fourier transform of the resulting sequence.

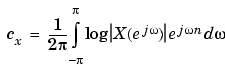
The toolbox function rceps performs this operation, returning the real cepstrum for a sequence x. The returned sequence is a real-valued vector the same size as the input vector:

```
y = rceps(x)
```

By definition, you cannot reconstruct the original sequence from its real cepstrum transformation, as the real cepstrum is based only on the magnitude of the Fourier transform for the sequence (see Oppenheim and Schafer [3]). The rceps function also returns a unique minimum-phase sequence that has the same real cepstrum as x.. To obtain both the real cepstrum and the minimum phase reconstruction for a sequence, use

```
[y,ym] = rceps(x)
```

where y is the real cepstrum and ym is the minimum phase reconstruction of x. The following example shows that one output of rceps is a unique minimum-phase sequence with the same real cepstrum as x.

y = [4 1 5];                      % Non-minimum phase sequence
[xhat,yhat] = rceps(y);
xhat2= rceps(yhat); 
[xhat' xhat2'] 

ans =
    1.6225    1.6225
    0.3400    0.3400
    0.3400    0.3400

Resampling Inverse Complex Cepstrum