Discrete Cosine Transform :: Special Topics (Signal Processing Toolbox)

Signal Processing Toolbox

Discrete Cosine Transform

The toolbox function dct computes the unitary discrete cosine transform, or DCT, for an input vector or matrix. Mathematically, the unitary DCT of an input sequence x is

where

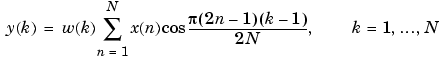
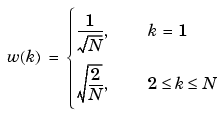
The DCT is closely related to the discrete Fourier transform; the DFT is actually one step in the computation of the DCT for a sequence. The DCT, however, has better energy compaction properties, with just a few of the transform coefficients representing the majority of the energy in the sequence. The energy compaction properties of the DCT make it useful in applications such as data communications.

The function idct computes the inverse DCT for an input sequence, reconstructing a signal from a complete or partial set of DCT coefficients. The inverse discrete cosine transform is

where

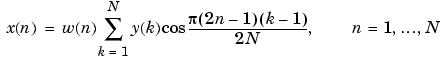
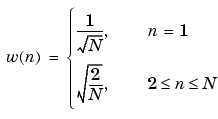
Because of the energy compaction mentioned above, it is possible to reconstruct a signal from only a fraction of its DCT coefficients. For example, generate a 25 Hz sinusoidal sequence, sampled at 1000 Hz:

```
t = (0:1/999:1);
x = sin(2*pi*25*t);
```

Compute the DCT of this sequence and reconstruct the signal using only those components with value greater than 0.1 (64 of the original 1000 DCT coefficients):

y = dct(x)                   % Compute DCT
y2 = find(abs(y) < 0.9);  % Use 17 coefficients
y(y2) = zeros(size(y2));     % Zero out points < 0.9
z = idct(y);                 % Reconstruct signal using inverse DCT

Plot the original and reconstructed sequences:

subplot(2,1,1); plot(t,x);
title('Original Signal')
subplot(2,1,2); plot(t,z), axis([0 1 -1 1])
title('Reconstructed Signal')

One measure of the accuracy of the reconstruction is

```
norm(x-z)/norm(x)
```

that is, the norm of the difference between the original and reconstructed signals, divided by the norm of the original signal. In this case, the relative error of reconstruction is 0.1443. The reconstructed signal retains approximately 85% of the energy in the original signal.

Chirp z-Transform Hilbert Transform