Signal Processing Toolbox

Correlation and Covariance

The functions xcorr and xcov estimate the cross-correlation and cross-covariance sequences of random processes. They also handle autocorrelation and autocovariance as special cases.

The true cross-correlation sequence is a statistical quantity defined as

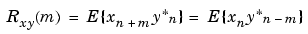
where x_n and y_n are stationary random processes, 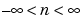, and E{·} is the expected value operator. The covariance sequence is the mean-removed cross-correlation sequence

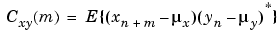
or, in terms of the cross-correlation,

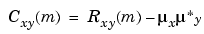
In practice, you must estimate these sequences, because it is possible to access only a finite segment of the infinite-length random process. A common estimate based on N samples of x_n and y_n is the deterministic cross-correlation sequence (also called the time-ambiguity function)

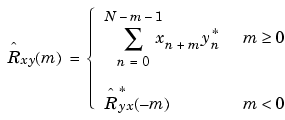
where we assume for this discussion that x_n and y_n are indexed from 0 to N-1, and 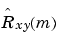from -(N-1) to N-1. The xcorr function evaluates this sum with an efficient FFT-based algorithm, given inputs x_n and y_n stored in length N vectors x and y. Its operation is equivalent to convolution with one of the two subsequences reversed in time.

For example:

• x = [1 1 1 1 1]';
  y = x;
  xyc = xcorr(x,y)
  xyc =
      1.0000
      2.0000
      3.0000
      4.0000
      5.0000
      4.0000
      3.0000
      2.0000
      1.0000
  

Notice that the resulting sequence length is one less than twice the length of the input sequence. Thus, the Nth element is the correlation at lag 0. Also notice the triangular pulse of the output that results when convolving two square pulses.

The xcov function estimates autocovariance and cross-covariance sequences. This function has the same options and evaluates the same sum as xcorr, but first removes the means of x and y.

Statistical Signal Processing

Bias and Normalization

© 1994-2005 The MathWorks, Inc.