ss2sos (Signal Processing Toolbox)

Convert digital filter state-space parameters to second-order sections form

Syntax

[sos,g] = ss2sos(A,B,C,D)
[sos,g] = ss2sos(A,B,C,D,iu)
[sos,g] = ss2sos(A,B,C,D,'order')
[sos,g] = ss2sos(A,B,C,D,iu,'order')
[sos,g] = ss2sos(A,B,C,D,iu,'order','scale')
sos = ss2sos(...)

Description

ss2sos converts a state-space representation of a given digital filter to an equivalent second-order section representation.

[sos,g] = ss2sos(A,B,C,D) finds a matrix sos in second-order section form with gain g that is equivalent to the state-space system represented by input arguments A, B, C, and D. The input system must be single output and real. sos is an L-by-6 matrix

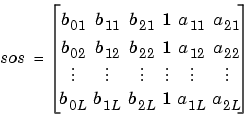
whose rows contain the numerator and denominator coefficients b_ik and a_ik of the second-order sections of H(z).

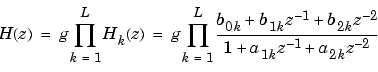
[sos,g] = ss2sos(A,B,C,D,iu) specifies a scalar iu that determines which input of the state-space system A, B, C, D is used in the conversion. The default for iu is 1.

[sos,g] = ss2sos(A,B,C,D,'order') and

[sos,g] = ss2sos(A,B,C,D,iu,'order') specify the order of the rows in sos, where 'order' is

'down', to order the sections so the first row of sos contains the poles closest to the unit circle
'up', to order the sections so the first row of sos contains the poles farthest from the unit circle (default)

The zeros are always paired with the poles closest to them.

[sos,g] = ss2sos(A,B,C,D,iu,'order','scale') specifies the desired scaling of the gain and the numerator coefficients of all second-order sections, where 'scale' is

'none', to apply no scaling (default)
'inf', to apply infinity-norm scaling
'two', to apply 2-norm scaling

Using infinity-norm scaling in conjunction with up-ordering minimizes the probability of overflow in the realization. Using 2-norm scaling in conjunction with down-ordering minimizes the peak round-off noise.

Note Infinity-norm and 2-norm scaling are appropriate only for direct-form II implementations.

sos = ss2sos(...) embeds the overall system gain, g, in the first section, H₁(z), so that

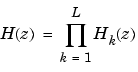
Note Embedding the gain in the first section when scaling a direct-form II structure is not recommended and may result in erratic scaling. To avoid embedding the gain, use ss2sos with two outputs.

Examples

Find a second-order section form of a Butterworth lowpass filter:

[A,B,C,D] = butter(5,0.2);
sos = ss2sos(A,B,C,D)
sos =
    0.0013    0.0013         0    1.0000   -0.5095         0
    1.0000    2.0008    1.0008    1.0000   -1.0966    0.3554
    1.0000    1.9979    0.9979    1.0000   -1.3693    0.6926

Algorithm

ss2sos uses a four-step algorithm to determine the second-order section representation for an input state-space system:

It finds the poles and zeros of the system given by A, B, C, and D.
It uses the function zp2sos, which first groups the zeros and poles into complex conjugate pairs using the cplxpair function. zp2sos then forms the second-order sections by matching the pole and zero pairs according to the following rules:

Match the poles closest to the unit circle with the zeros closest to those poles.
Match the poles next closest to the unit circle with the zeros closest to those poles.
Continue until all of the poles and zeros are matched.

ss2sos groups real poles into sections with the real poles closest to them in absolute value. The same rule holds for real zeros.

It orders the sections according to the proximity of the pole pairs to the unit circle. ss2sos normally orders the sections with poles closest to the unit circle last in the cascade. You can tell ss2sos to order the sections in the reverse order by specifying the 'down' flag.
ss2sos scales the sections by the norm specified in the 'scale' argument. For arbitrary H(), the scaling is defined by

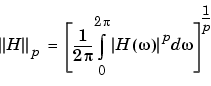
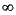where p can be either or 2. See the references for details. This scaling is an attempt to minimize overflow or peak round-off noise in fixed point filter implementations.

Diagnostics

If there is more than one input to the system, ss2sos gives the following error message:

State-space system must have only one input.

See Also

cplxpair, sos2ss, ss2tf, ss2zp, tf2sos, zp2sos

References

[1] Jackson, L.B., Digital Filters and Signal Processing, 3rd ed., Kluwer Academic Publishers, Boston, 1996. Chapter 11.

[2] Mitra, S.K., Digital Signal Processing: A Computer-Based Approach, McGraw-Hill, New York, 1998. Chapter 9.

[3] Vaidyanathan, P.P.,"Robust Digital Filter Structures," Handbook for Digital Signal Processing, S.K. Mitra and J.F. Kaiser, ed., John Wiley & Sons, New York, 1993, Chapter 7.

square ss2tf