appcoef (Wavelet Toolbox)

1-D approximation coefficients

Syntax

A = appcoef(C,L,'wname',N)
A = appcoef(C,L,'wname')
A = appcoef(C,L,Lo_R,Hi_R)
A = appcoef(C,L,Lo_R,Hi_R,N)

Description

appcoef is a one-dimensional wavelet analysis function.

appcoef computes the approximation coefficients of a one-dimensional signal.

A = appcoef(C,L,'wname',N) computes the approximation coefficients at level N using the wavelet decomposition structure [C,L] (see wavedec for more information).

'wname' is a string containing the wavelet name. Level N must be an integer such that 0 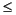N 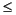length(L)-2.

A = appcoef(C,L,'wname') extracts the approximation coefficients at the last level: length(L)-2.

Instead of giving the wavelet name, you can give the filters.

For A = appcoef(C,L,Lo_R,Hi_R) or A = appcoef(C,L,Lo_R,Hi_R,N), Lo_R is the reconstruction low-pass filter and Hi_R is the reconstruction high-pass filter (see wfilters for more information).

Examples

% The current extension mode is zero-padding (see dwtmode).

% Load a one-dimensional signal. 
load leleccum; s = leleccum(1:3920); 

% Perform decomposition at level 3 of s using db1. 
[c,l] = wavedec(s,3,'db1');

% Extract approximation coefficients at level 3, from the 
% wavelet decomposition structure [c,l]. 
ca3 = appcoef(c,l,'db1',3);
% Using some plotting commands,
% the following figure is generated.

Algorithm

The input vectors C and L contain all the information about the signal decomposition.

Let NMAX = length(L)-2; then C = [A(NMAX) D(NMAX) ... D(1)] where A and the D are vectors.

If N = NMAX, then a simple extraction is done; otherwise, appcoef computes iteratively the approximation coefficients using the inverse wavelet transform.

See Also
detcoef, wavedec

allnodes appcoef2