Wavelet Toolbox

Five Easy Steps to a Continuous Wavelet Transform

The continuous wavelet transform is the sum over all time of the signal multiplied by scaled, shifted versions of the wavelet. This process produces wavelet coefficients that are a function of scale and position.

It's really a very simple process. In fact, here are the five steps of an easy recipe for creating a CWT:

1. Take a wavelet and compare it to a section at the start of the original signal.
2. Calculate a number, C, that represents how closely correlated the wavelet is with this section of the signal. The higher C is, the more the similarity. More precisely, if the signal energy and the wavelet energy are equal to one, C may be interpreted as a correlation coefficient.

1. Note that the results will depend on the shape of the wavelet you choose.
   
   

3. Shift the wavelet to the right and repeat steps 1 and 2 until you've covered the whole signal.
   
   
4. Scale (stretch) the wavelet and repeat steps 1 through 3.
   
   
5. Repeat steps 1 through 4 for all scales.

When you're done, you'll have the coefficients produced at different scales by different sections of the signal. The coefficients constitute the results of a regression of the original signal performed on the wavelets.

How to make sense of all these coefficients? You could make a plot on which the x-axis represents position along the signal (time), the y-axis represents scale, and the color at each x-y point represents the magnitude of the wavelet coefficient C. These are the coefficient plots generated by the graphical tools.

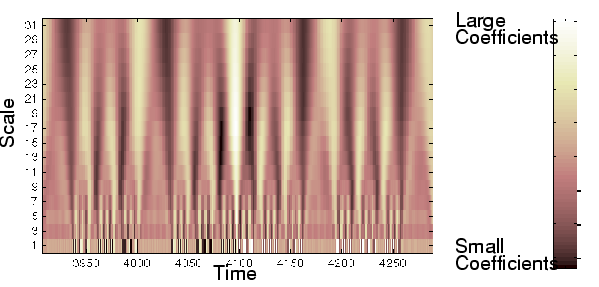
These coefficient plots resemble a bumpy surface viewed from above. If you could look at the same surface from the side, you might see something like this:

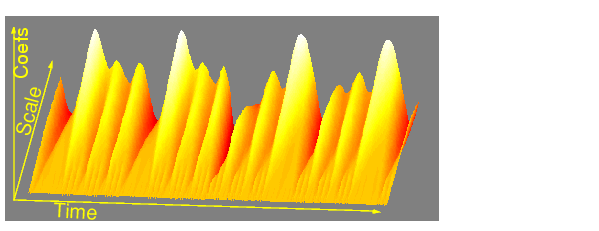
The continuous wavelet transform coefficient plots are precisely the time-scale view of the signal we referred to earlier. It is a different view of signal data from the time-frequency Fourier view, but it is not unrelated.

Shifting

Scale and Frequency

© 1994-2005 The MathWorks, Inc.