Wavelet Toolbox

Example 1: A Sum of Sines

Analyzing wavelet: db3

Decomposition levels: 5

The signal is composed of the sum of three sines: slow, medium, and rapid. With regard to the sampling period equal to 1, the periods are approximately 200, 20, and 2 respectively. We should, therefore, see this later period in D₁, the medium sine in D₄, and the slow sine in A₄. The slight differences that can be observed on the decompositions can be attributed to the sampling period. The scale of the approximation charts is 2, 4, or 10 times larger than that of the details. D₁ contains primarily the components whose period is situated between 1 and 2 (i.e., the rapid sine), but this period is not visible at the scale that is used for the graph. Zooming in on D₁ reveals that each "belly" is composed of 10 oscillations, and can be used to estimate the period. We find that the period is close to 2. D₂ is very small. This is also seen in the approximations: the first two resemble one another, since .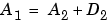

The detail D₃ and, to an even greater extent, the detail D₄ contain the medium sine. We notice that there is a breakdown between approximations 3 and 4.

Approximations A₁ to A₃ can be used to estimate the period of the medium sine. Now, only the slow sine, which appears in A₄, remains to be determined. The distance between two successive maximums is equal to 200, which is the period of the slow sine. This latter sine is still visible in A₅, but will disappear from the approximation and move into the details at level 8.

Example 1: A Sum of Sines
Addressed topics	Detecting breakdown points Detecting long-term evolution Identifying pure frequencies The effect of a wavelet on a sine Details and approximations: a signal moves from an approximation to a detail The level at which characteristics appear
Further exploration	Compare with a Fourier analysis. Change the frequencies. Analyze other linear combinations.

Advice to the Reader

Example 2: A Frequency Breakdown

© 1994-2005 The MathWorks, Inc.