Wavelet Toolbox

Example 3: Uniform White Noise

Analyzing wavelet: db3

Decomposition levels: 5

At all levels we encounter noise-type signals that are clearly irregular. This is because all the frequencies carry the same energy. The variances, however, decrease regularly between one level and the next as can be seen reading the detail chart (on the right) and the approximations (on the left).

The variance decreases two-fold between one level and the next, i.e., variance(D_j) = variance(D_{j - 1}) / 2. Lastly, it should be noted that the details and approximations are not white noise, and that these signals are increasingly interdependent as the resolution decreases. On the other hand, the wavelet coefficients are random, noncorrelated variables. This property is not evident on the reconstructed signals shown here, but it can be guessed at from the representation of the coefficients.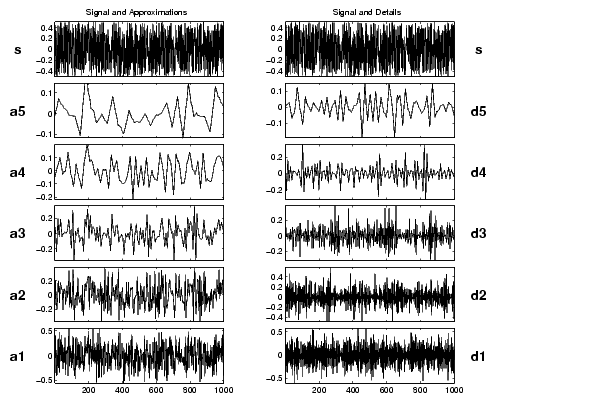

Example 3: Uniform White Noise
Addressed topics	Processing noise The shapes of the decomposition values The evolution of these shapes according to level; the correlation increases, the variance decreases
Further exploration	Compare the frequencies included in the details with those in the approximations. Study the values of the coefficients and their distribution. On the continuous analysis, identify the chaotic aspect of the colors. Replace the uniform white noise by a Gaussian white noise or other noise.

Example 2: A Frequency Breakdown

Example 4: Colored AR(3) Noise

© 1994-2005 The MathWorks, Inc.