Wavelet Toolbox

Inverse Discrete Stationary Wavelet Transform (ISWT)

Each 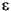-decimated DWT corresponding to a given 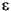can be inverted.

To reconstruct the original signal using a given 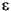-decimated DWT characterized by [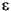₁,...,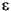_J], we can use the abstract algorithm

• FOR j = J:-1:1
    A(j-1, 1,...,j-1) = ...
    idwt(A(j,1,...,j),D(S,1,...,j)],wname,'mode','per','shift',j);
  END
  

For each choice of 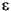= (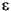₁,...,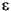_J), we obtain the original signal A(0), starting from slightly different decompositions, and capturing in different ways the main features of the analyzed signal.

The idea of the inverse discrete stationary wavelet transform is to average the inverses obtained for every 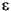-decimated DWT. This can be done recursively, starting from level J down to level 1.

The ISWT is obtained with the following abstract algorithm:

• FOR j = J:-1:1
      X0 = idwt(A(j,1,...,j),D(j,1,...,j)],wname, ...
              'mode','per','shift',0);
      X1 = idwt(A(j,1,...,j),D(j,1,...,j)],wname, ...
              'mode','per','shift',1);
      X1 = wshift('1D',X1,1);
      A(j-1, 1,...,j-1) = (X0+X1)/2;
  END
  

Along the same lines, this can be extended to the 2-D case.

How to Calculate the -Decimated DWT: SWT

More About SWT

© 1994-2005 The MathWorks, Inc.