Wavelet Toolbox

Lifting Background

The DWT is defined by four filters as described in The Fast Wavelet Transform (FWT) Algorithm. Two main properties of interest are

• The perfect reconstruction property
• The link with "true" wavelets (how to generate, starting from the filters, orthogonal or biorthogonal bases of the space of the functions of finite energy)

To illustrate the perfect reconstruction property, the following filter bank contains two decomposition filters, h_a, g_a and two reconstruction filters h_s, g_s..

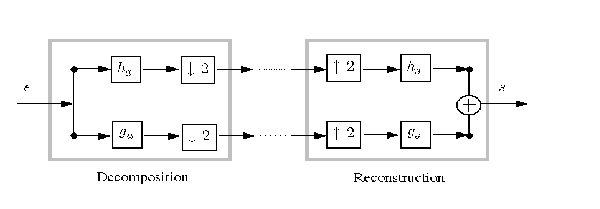
The perfect reconstruction property can be expressed by the equality s = e (up to an eventual shift or delay) where the two signals s and e are defined in the following figure:

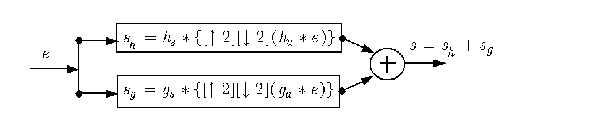
This leads to the following two conditions referred to as perfect reconstruction(PR):

• H_s(z) H_a(z^-1) + G_s(z) G_a(z^-1) = 2 z^-d

• H_s(z) H_a(-z^-1) + G_s(z) G_a(-z^-1) = 0

where H_s(z), G_s(z) are the z-transforms of the filters h_s, g_s respectively and H_a(-z^-1) and G_a(-z^-1) are the z-transforms of h_a, g_a respectively.

The first condition is usually (incorrectly) called the perfect reconstruction condition and the second is the anti-aliasing condition.

Below we refer to the four filters (or equivalently four z-transforms) verifying the (PR) conditions as biorthogonal quadruplets.

The principle of lifting is to generate from a given biorthogonal quadruplet a new one by applying a finite sequence of primal or dual elementary lifting steps (ELS).

A primal ELS generates from the biorthogonal quadruplet (H_a,G_a,H_s,G_s), a new one (H_a^N,G_a,H_s,G_s^N) by

• H_a^N (z) = H_a(z) - G_a(z) S(z^-2)

• G_s^N (z) = G_s(z) + H_s(z) S(z²)

where S is any Laurent polynomial.

Let us recall that C is a Laurent polynomial if

• C(z) = c₁ z^pmax + c₂ z^pmax-1 + ... + c_end z^pmin

involving positive and negative integer powers of z. The degree of C is defined as (pmax-pmin).

Similarly, a dual ELS generates from the same initial biorthogonal quadruplet, a new one (H_a,G_a^N,H_s^H,G_s) by

• H_s^N (z) = H_s(z) + G_s(z) T(z²)

• G_a^N (z) = G_a(z) - H_a(z) T(z^-2)

where T is any Laurent polynomial.

These new quadruplets verify the perfect reconstruction conditions (PR). Note that even if the initial biorthogonal quadruplet is associated with "true" wavelets, the new ones are not automatically associated with "true" wavelets but remain useful for discrete wavelet transform of sequences instead of functions.

The previous results are sufficient to generate lifted quadruplets. Nevertheless, by introducing the polyphase matrix, interesting theoretical and algorithmic results can be derived. The synthesis polyphase matrix P associated with the biorthogonal quadruplet (H_a,G_a,H_s,G_s) is the 2-by-2 matrix defined (using the MATLAB conventions) by

• P(z) = [ even(H_s)(z) even(G_s)(z) ; odd(H_s)(z) odd(G_s)(z) ]

where

• even(C)(z²) = (C(z) + C(-z)) / 2

• odd(C)(z²) = (C(z) - C(-z)) / 2z^-1

Then after a primal lifting the new polyphase matrix P^N is obtained simply from P the initial one by:

• P^N(z) = P(z) * [1 S(z) ; 0 1]

and after a dual lifting by:

• P^N(z) = P(z) * [1 0 ; T(z) 1]

P itself can be decomposed, up to a normalization, as a product of matrices of the form [1 S(z) ; 0 1] or [1 0 ; T(z) 1] as soon as P is associated with a biorthogonal quadruplet. This form leads to the efficient polyphase algorithm (see [StrN96] in References) because the inverses of such elementary matrices are explicit.

Another useful consequence is that any biorthogonal quadruplet can be obtained by a sequence of ELS, up to a normalization, starting from a particular seed called the "lazy" wavelet (which is not a "true" wavelet and which simply separates odd and even samples of the filter bank input signal).

So, in the Wavelet Toolbox, the key structure to perform what we commonly call the lifting wavelet transform (LWT) is a lifting scheme, which is simply a sequence of ELS and normalization steps.

Lifting Method for Constructing Wavelets

Lifting Functions

© 1994-2005 The MathWorks, Inc.