| Wavelet Toolbox | |
Coiflet Wavelets: coifN
In coifN, N is the order. Some authors use 2N instead of N. For the coiflet construction, see [Dau92] pages 258-259. By typing waveinfo('coif') at the MATLAB command prompt, you can obtain a survey of the main properties of this family.
Figure 6-14: Coiflets coif3 on the Left and coif5 on the Right
Built by Daubechies at the request of Coifman, the function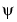 
has 2N moments equal to 0 and, what is more unusual, the function 
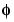has 2N-1 moments equal to 0. The two functions have a support of length 6N-1.
The coifN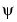 
and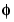 
are much more symmetrical than the dbNs. With respect to the support length, coifN has to be compared to db3N or sym3N. With respect to the number of vanishing moments of 
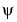, coifN has to be compared to db2N or sym2N.
If s is a sufficiently regular continuous time signal, for large j the coefficient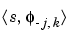 
is approximated by 
.
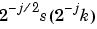If s is a polynomial of degree d, d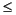 
N - 1, then the approximation becomes an equality. This property is used, connected with sampling problems, when calculating the difference between an expansion over the 
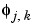of a given signal and its sampled version.
| | Symlet Wavelets: symN | Biorthogonal Wavelet Pairs: biorNr.Nd | |
© 1994-2005 The MathWorks, Inc.
