qmf (Wavelet Toolbox)

Quadrature mirror filter

Syntax

```
Y = qmf(X,P)
Y = qmf(X)
```

Description

Y = qmf(X,P) changes the signs of the even index entries of the reversed vector filter coefficients X if P is even. If P is odd the same holds for odd index entries. Y = qmf(X) is equivalent to Y = qmf(X,0).

Let x be a finite energy signal. Two filters F₀ and F₁ are quadrature mirror filters (QMF) if, for any x,

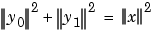
where y₀ is a decimated version of the signal x filtered with F₀ so y₀is defined by x₀= F₀(x) and y₀(n) = x₀(2n), and similarly, y₁ is defined by x₁ = F₁(x) and
y₁(n) = x₁(2n). This property ensures a perfect reconstruction of the associated two-channel filter banks scheme (See Strang-Nguyen p. 103).

For example, if F₀ is a Daubechies scaling filter and F₁ = qmf(F₀), then the transfer functions F₀(z) and F₁(z) of the filters F₀ and F₁ satisfy the condition (see the example for db10):

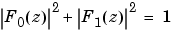
Examples

% Load scaling filter associated with an orthogonal wavelet. 
load db10; 
subplot(321); stem(db10); title('db10 low-pass filter');

% Compute the quadrature mirror filter. 
qmfdb10 = qmf(db10); 
subplot(322); stem(qmfdb10); title('QMF db10 filter');

% Check for frequency condition (necessary for orthogonality):
% abs(fft(filter))^2 + abs(fft(qmf(filter))^2 = 1 at each 
% frequency. 
m = fft(db10); 
mt = fft(qmfdb10); 
freq = [1:length(db10)]/length(db10); 
subplot(323); plot(freq,abs(m)); 
title('Transfer modulus of db10')
subplot(324); plot(freq,abs(mt)); 
title('Transfer modulus of QMF db10')
subplot(325); plot(freq,abs(m).^2 + abs(mt).^2); 
title('Check QMF condition for db10 and QMF db10') 
xlabel(' abs(fft(db10))^2 + abs(fft(qmf(db10))^2 = 1')

% Editing some graphical properties,
% the following figure is generated.


% Check for orthonormality. 
df = [db10;qmfdb10]*sqrt(2); 
id = df*df'

id =
    1.0000 0.0000 
    0.0000 1.0000

References

Strang, G.; T. Nguyen (1996), Wavelets and Filter Banks, Wellesley-Cambridge Press.

plot rbiowavf