wden (Wavelet Toolbox)

Automatic 1-D de-noising

Syntax

[XD,CXD,LXD] = wden(X,TPTR,SORH,SCAL,N,'wname')
[XD,CXD,LXD] = wden(C,L,TPTR,SORH,SCAL,N,'wname')

Description

wden is a one-dimensional de-noising function.

wden performs an automatic de-noising process of a one-dimensional signal using wavelets.

[XD,CXD,LXD] = wden(X,TPTR,SORH,SCAL,N,'wname') returns a de-noised version XD of input signal X obtained by thresholding the wavelet coefficients.

Additional output arguments [CXD,LXD] are the wavelet decomposition structure (see wavedec for more information) of the de-noised signal XD.

TPTR string contains the threshold selection rule:

'rigrsure' use the principle of Stein's Unbiased Risk

'heursure' is an heuristic variant of the first option

'sqtwolog' for universal threshold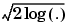

'minimaxi' for minimax thresholding (see thselect for more information)

SORH ('s' or 'h') is for soft or hard thresholding (see wthresh for more information).

SCAL defines multiplicative threshold rescaling:

'one' for no rescaling

'sln' for rescaling using a single estimation of level noise based on first-level coefficients

'mln' for rescaling done using level-dependent estimation of level noise

Wavelet decomposition is performed at level N and 'wname' is a string containing the name of the desired orthogonal wavelet (see wmaxlev and wfilters for more information).

[XD,CXD,LXD] = wden(C,L,TPTR,SORH,SCAL,N,'wname') returns the same output arguments, using the same options as above, but obtained directly from the input wavelet decomposition structure [C,L] of the signal to be de-noised, at level N and using 'wname' orthogonal wavelet.

The underlying model for the noisy signal is basically of the following form:

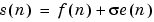
where time n is equally spaced.

In the simplest model, suppose that e(n) is a Gaussian white noise N(0,1) and the noise level 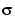a is supposed to be equal to 1.

The de-noising objective is to suppress the noise part of the signal s and to recover f.

The de-noising procedure proceeds in three steps:

Decomposition. Choose a wavelet, and choose a level N. Compute the wavelet decomposition of the signal s at level N.
Detail coefficients thresholding. For each level from 1 to N, select a threshold and apply soft thresholding to the detail coefficients.
Reconstruction. Compute wavelet reconstruction based on the original approximation coefficients of level N and the modified detail coefficients of levels from 1 to N.

More details about threshold selection rules can be found in the "De-noising" section of Chapter 6, "Advanced Concepts", in the User's Guide, and in the help of the thselect function. Let us point out that

The detail coefficients vector is the superposition of the coefficients of f and the coefficients of e, and that the decomposition of e leads to detail coefficients that are standard Gaussian white noises.
Minimax and SURE threshold selection rules are more conservative and are more convenient when small details of function f lie in the noise range. The two other rules remove the noise more efficiently. The option 'heursure' is a compromise.

In practice, the basic model cannot be used directly. This section examines the options available, to deal with model deviations. The remaining parameter scal has to be specified. It corresponds to threshold rescaling methods.

Option scal = 'one' corresponds to the basic model.
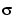In general, you can ignore the noise level that must be estimated. The detail coefficients CD₁ (the finest scale) are essentially noise coefficients with standard deviation equal to . The median absolute deviation of the coefficients is a robust estimate of 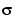. The use of a robust estimate is crucial for two reasons. The first is that if level 1 coefficients contain f details, these details are concentrated in few coefficients. The second reason is to avoid signal end effects, which are pure artifacts due to computations on the edges.
Option scal = 'sln' handles threshold rescaling using a single estimation of level noise based on the first-level coefficients.
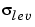When you suspect a nonwhite noise e, thresholds must be rescaled by a level dependent estimation of the level noise. The same kind of strategy is used by estimating level by level. This estimation is implemented in M-file wnoisest, which handles the wavelet decomposition structure of the original signal s directly.
Option scal = 'mln' handles threshold rescaling using a level-dependent estimation of the level noise.

Examples

% The current extension mode is zero-padding (see dwtmode).

% Set signal to noise ratio and set rand seed. 
snr = 3; init = 2055615866; 

% Generate original signal and a noisy version adding 
% a standard Gaussian white noise. 
[xref,x] = wnoise(3,11,snr,init);

% De-noise noisy signal using soft heuristic SURE thresholding 
% and scaled noise option, on detail coefficients obtained 
% from the decomposition of x, at level 5 by sym8 wavelet. 
lev = 5;
xd = wden(x,'heursure','s','one',lev,'sym8');

% Plot signals. 
subplot(611), plot(xref), axis([1 2048 -10 10]); 
title('Original signal'); 
subplot(612), plot(x), axis([1 2048 -10 10]); 
title(['Noisy signal - Signal to noise ratio = ',... 
num2str(fix(snr))]); 
subplot(613), plot(xd), axis([1 2048 -10 10]); 
title('De-noised signal - heuristic SURE'); 

% De-noise noisy signal using soft SURE thresholding 
xd = wden(x,'heursure','s','one',lev,'sym8');

% Plot signal. 
subplot(614), plot(xd), axis([1 2048 -10 10]); 
title('De-noised signal - SURE');

% De-noise noisy signal using fixed form threshold with 
% a single level estimation of noise standard deviation. 
xd = wden(x,'sqtwolog','s','sln',lev,'sym8');

% Plot signal. 
subplot(615), plot(xd), axis([1 2048 -10 10]); 
title('De-noised signal - Fixed form threshold');

% De-noise noisy signal using minimax threshold with 
% a multiple level estimation of noise standard deviation. 
xd = wden(x,'minimaxi','s','sln',lev,'sym8');

% Plot signal. 
subplot(616), plot(xd), axis([1 2048 -10 10]); 
title('De-noised signal - Minimax');

% If many trials are necessary, it is better to perform 
% decomposition once and threshold it many times:
 
% decomposition. 
[c,l] = wavedec(x,lev,'sym8');
 
% threshold the decomposition structure [c,l].
xd = wden(c,l,'minimaxi','s','sln',lev,'sym8');

% Editing some graphical properties,
% the following figure is generated.

See Also
thselect, wavedec, wdencmp, wfilters, wthresh

References

Antoniadis, A.; G. Oppenheim, Eds. (1995), Wavelets and statistics, 103,
Lecture Notes in Statistics, Springer Verlag.

Donoho, D.L. (1993), "Progress in wavelet analysis and WVD: a ten minute tour," in Progress in wavelet analysis and applications, Y. Meyer, S. Roques, pp. 109-128. Frontières Ed.

Donoho, D.L.; I.M. Johnstone (1994), "Ideal spatial adaptation by wavelet shrinkage," Biometrika, vol 81, pp. 425-455.

Donoho, D.L. (1995), "De-noising by soft-thresholding," IEEE Trans. on Inf. Theory, 41, 3, pp. 613-627.

Donoho, D.L.; I.M. Johnstone, G. Kerkyacharian, D. Picard (1995), "Wavelet shrinkage: asymptotia," Jour. Roy. Stat. Soc., series B, vol. 57, no. 2, pp. 301-369.

wdcbm2 wdencmp