

| Wavelet Toolbox |   |
Syntax
Description
E = wentropy(X,T,P) returns the entropy E of the vector or matrix input X. In both cases, output E is a real number.
E = wentropy(X,T) is equivalent to E = wentropy(X,T,0).
T is a string containing the type of entropy and P is an optional parameter depending on the value of T.
Functionals verifying an additive-type property are well suited for efficient searching of binary-tree structures and the fundamental splitting property of the wavelet packets decomposition. Classical entropy-based criteria match these conditions and describe information-related properties for an accurate representation of a given signal. Entropy is a common concept in many fields, mainly in signal processing. The following example lists different entropy criteria, many others are available and can be easily integrated. In the following expressions, s is the signal and (si)i the coefficients of s in an orthonormal basis.
The entropy E must be an additive cost function such that E(0) = 0 and
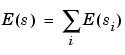
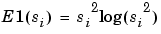 so
so 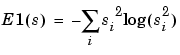
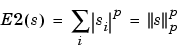
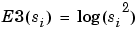 so
so 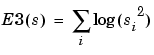
E4(si) = 1 if |si| > p and 0 elsewhere so E4(s) = #{i such that |si| > p} is the number of time instants when the signal is greater than a threshold p.
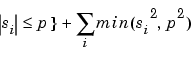
For more information, see the section entitled "Using wavelet packets for compression and de-noising" in Chapter 6, "Advanced Concepts", of the User's Guide.
Examples
% The current extension mode is zero-padding (see dwtmode).
% Generate initial signal.
x = randn(1,200);
% Compute Shannon entropy of x.
e = wentropy(x,'shannon')
e =
-142.7607
% Compute log energy entropy of x.
e = wentropy(x,'log energy')
e =
-281.8975
% Compute threshold entropy of x
% with threshold equal to 0.2.
e = wentropy(x,'threshold',0.2)
e =
162
% Compute Sure entropy of x
% with threshold equal to 3.
e = wentropy(x,'sure',3)
e =
-0.6575
% Compute norm entropy of x with power equal to 1.1.
e = wentropy(x,'norm',1.1)
e =
160.1583
% Compute user entropy of x with a user defined
% function: userent for example.
% This function must be an M-file, with first line
% of the following form:
%
% function e = userent(x)
%
% where x is a vector and e is a real number.
% Then a new entropy is defined and can be used typing:
%
% e = wentropy(x,'user','userent')
%
% or more directly
%
% e = wentropy(x,'userent')
References
Coifman, R.R.; M.V. Wickerhauser (1992), "Entropy-based Algorithms for best basis selection," IEEE Trans. on Inf. Theory, vol. 38, 2, pp. 713-718.
Donoho, D.L.; I.M. Johnstone, "Ideal de-noising in an orthonormal basis chosen from a library of bases," C.R.A.S. Paris, Ser. I, t. 319, pp. 1317-1322.
 | wenergy2 | wextend |  |
© 1994-2005 The MathWorks, Inc.