wrcoef2 (Wavelet Toolbox)

Reconstruct single branch from 2-D wavelet coefficients

Syntax

X = wrcoef2('type',C,S,'wname',N)
X = wrcoef2('type',C,S,Lo_R,Hi_R,N)
X = wrcoef2('type',C,S,'wname')
X = wrcoef2('type',C,S,Lo_R,Hi_R)

Description

wrcoef2 is a two-dimensional wavelet analysis function. wrcoef2 reconstructs the coefficients of an image.

X = wrcoef2('type',C,S,'wname',N) computes the matrix of reconstructed coefficients of level N, based on the wavelet decomposition structure [C,S] (see wavedec2 for more information).

'wname' is a string containing the name of the wavelet (see wfilters for more information). If 'type' = 'a', approximation coefficients are reconstructed; otherwise if 'type' = 'h' ('v' or 'd', respectively), horizontal (vertical or diagonal, respectively) detail coefficients are reconstructed.

Level N must be an integer such that 0 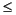N 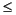size(S,1)-2 if 'type' = 'a' and such that 1 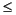N 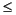size(S,1)-2 if 'type' = 'h', 'v' or 'd'.

Instead of giving the wavelet name, you can give the filters.

For X = wrcoef2('type',C,S,Lo_R,Hi_R,N), Lo_R is the reconstruction low-pass filter and Hi_R is the reconstruction high-pass filter.

X = wrcoef2('type',C,S,'wname') or X = wrcoef2('type',C,S,Lo_R,Hi_R) reconstruct coefficients of maximum level N = size(S,1)-2.

Examples

% The current extension mode is zero-padding (see dwtmode).

% Load an image. 
load woman;
% X contains the loaded image.

% Perform decomposition at level 2 
% of X using sym5. 
[c,s] = wavedec2(X,2,'sym5');

% Reconstruct approximations at 
% levels 1 and 2, from the wavelet 
% decomposition structure [c,s]. 
a1 = wrcoef2('a',c,s,'sym5',1); 
a2 = wrcoef2('a',c,s,'sym5',2);

% Reconstruct details at level 2, 
% from the wavelet decomposition 
% structure [c,s]. 
% 'h' is for horizontal, 
% 'v' is for vertical, 
% 'd' is for diagonal. 
hd2 = wrcoef2('h',c,s,'sym5',2); 
vd2 = wrcoef2('v',c,s,'sym5',2); 
dd2 = wrcoef2('d',c,s,'sym5',2);

% All these images are of same size sX. 
sX = size(X)

sX =
 256 256

sa1 = size(a1)

sa1 =
 256 256

shd2 = size(hd2)

shd2 =
 256 256

See Also

appcoef2, detcoef2, wavedec2

wrcoef wrev