Transforming Objects :: Handle Graphics Objects (Graphics)

Graphics

Transforming Objects

The hgtransform object's Matrix property enables you to apply a transform to all the hgtransform's children in unison. Typical transforms include rotation, translation, and scaling. You define a transform with a four-by-four transformation matrix, which is described in the following sections.

Creating a Transform Matrix

The makehgtform function simplifies the construction of matrices to perform rotation, translation, and scaling. See the Example -- Transforming a Hierarchy of Objects section for information on creating transform matrices using makehgtform.

Rotation

Rotation transforms rotate objects about the x-, y-, or z-axis, with positive angles rotating counterclockwise while sighting along the respective axis toward the origin. If the desired angle of rotation is 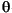theta , the following matrices define this rotation about the respective axis.

To create a transform matrix for rotation about an arbitrary axis, use the makehgtform function.

Translation

Translation transforms move objects with respect to their current locations. Specify the translation as distances t_x, t_y, and t_z in data space units. The following matrix shows the location of these elements in the transform matrix.

Scaling

Scaling transforms change the sizes of objects. Specify scale factors s_x_,s_y, and s_z and construct the following matrix.

The Default Transform

The default transform is the identity matrix, which you can create with the eye function. Here is the identity matrix:

See Undoing Transform Operations for related information.

Absolute vs. Relative Transforms

Transforms are specified in absolute terms, not relative to the current transform. For example, if you apply a transform that translates the hgtransform object 5 units in the x direction and then you apply another transform that translates it 4 units in the y direction, the resulting position of the object is 4 units in the y direction from its original position.

If you want transforms to accumulate, you must concatenate the individual transforms into a single matrix. See Combining Transforms into One Matrix for more information.

Combining Transforms into One Matrix

It is usually more efficient to combine various transform operations into one matrix by concatenating (multiplying) the individual matrices and setting the Matrix property to the result. Note that matrix multiplication is not commutative, so the order in which you multiply the matrices affects the result. For example, suppose you want to perform an operation that scales, translates, and then rotates. You would multiply the matrices as follows:

C = R*T*S % operations are performed from right to left

where S is the scaling matrix, T is the translation matrix, R is the rotation matrix, and C is the composite of the three operations. You then set the hgtransform object's Matrix property to C:

```
set(hgtransform_handle,'Matrix',C)
```

Note that the following sets of statements are not equivalent:

set(hgtransform_handle,'Matrix',C)% Transform as above
set(hgtransform_handle,'Matrix',eye(4) ) % Undo transform

versus

C = eye(4)*R*T*S % Multiply identity matrix as last step
set(hgtransform_handle,'Matrix',C)

Concatenating the identity matrix to other matrices has no effect on the composite matrix.

Undoing Transform Operations

Since transform operations are specified in absolute terms (not relative to the current transform), you can undo a series of transforms by setting the current transform to the identity matrix. For example, the following statement

set(hgtransform_handle,'Matrix',eye(4))

returns the object hgtransform_handle to its untransformed orientation.

Rotations Away From the Origin

Since rotations are performed about the origin, it is often necessary to translate the hgtransform object so that the desired axis of rotation is temporarily at the origin. After applying the rotation transform matrix, you then translate the hgtransform object back to its original position. The following example illustrates how to do this.

Suppose you want to rotate a surface about the y-axis at the center of the surface (the y-axis that passes through the point x = 20 in this example).

Note If you are using the MATLAB Help browser, you can run this example or open it in the MATLAB editor.

Create a surface and an hgtransform object. Parent the surface to the hgtransform object.
- ```
h = surf(peaks(40)); view(-20,30)
t = hgtransform;
set(h,'Parent',t)
```

The following picture shows the surface.

Create and set a y-axis rotation matrix to rotate the surface by -15 degrees.

ry_angle = -15*pi/180; % Convert to radians
Ry = makehgtform('yrotate',ry_angle);
set(t,'Matrix',Ry)

Notice that the surface rotated -15 degrees about the y-axis that passes through the origin. However, to rotate about the y-axis that passes through the point x = 20, you must translate the surface in x by 20 units.

Create two translation matrices, one to translate the surface -20 units in x and another to translate 20 units back. Concatenate the two translation matrices with the rotation matrix in the correct order and set the transform.
- ```
Tx1 = makehgtform('translate',[-20 0 0]);
Tx2 = makehgtform('translate',[20 0 0]);
set(t,'Matrix',Tx2*Ry*Tx1)
```

Group Objects Example -- Transforming a Hierarchy of Objects