Graphics

Three-Dimensional Stem Plots

stem3 displays 3-D stem plots extending from the xy-plane. With only one vector argument, MATLAB plots the stems in one row at x = 1 or y = 1, depending on whether the argument is a column or row vector. stem3 is intended to display data that you cannot visualize in a 2-D view.

Example - 3-D Stem Plot of an FFT

Fast Fourier transforms are calculated at points around the unit circle on the complex plane. So, it is interesting to visualize the plot around the unit circle. Calculating the unit circle

• th = (0:127)/128*2*pi;
  x = cos(th);
  y = sin(th);
  

and the magnitude frequency response of a step function

• f = abs(fft(ones(10,1),128));
  

displays the data using a 3-D stem plot, terminating the stems with filled diamond markers.

• stem3(x,y,f','d','fill')
  view([-65 30])
  
   
  

Label the Graph

Label the graph with the statements

• xlabel('Real')
  ylabel('Imaginary')
  zlabel('Amplitude')
  title('Magnitude Frequency Response')
  

To change the orientation of the view, turn on mouse-based 3-D rotation.

• rotate3d on
  

Example -- Combining Stem and Line Plots

Three-dimensional stem plots work well for visualizing discrete functions that do not output a large number of data points. For example, you can use stem3 to visualize the Laplace transform basis function,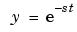, for a particular constant value of s.

• t = 0:.1:10;% Time limits
  s = 0.1+i;% Spiral rate
  y = exp(-s*t);% Compute decaying exponential 
  

Using t as magnitudes that increase with time, create a spiral with increasing height and draw a curve through the tops of the stems to improve definition.

• stem3(real(y),imag(y),t)
  hold on
  plot3(real(y),imag(y),t,'r')
  hold off
  view(-39.5,62)
  
   
  

Label the Graph

Add axes labels, with the statements

• xlabel('Real')
  ylabel('Imaginary')
  zlabel('Magnitude')
  

Combining Stem Plots with Line Plots

Stairstep Plots

© 1994-2005 The MathWorks, Inc.