More About Matrices and Arrays :: Matrices and Arrays (Getting Started)

Getting Started

More About Matrices and Arrays

This section shows you more about working with matrices and arrays, focusing on

Linear Algebra

Informally, the terms matrix and array are often used interchangeably. More precisely, a matrix is a two-dimensional numeric array that represents a linear transformation. The mathematical operations defined on matrices are the subject of linear algebra.

Dürer's magic square

A = [16     3     2    13
      5    10    11     8
      9     6     7    12
      4    15    14     1 ]

provides several examples that give a taste of MATLAB matrix operations. You have already seen the matrix transpose, A'. Adding a matrix to its transpose produces a symmetric matrix:

A + A'

ans =
    32     8    11    17
     8    20    17    23
    11    17    14    26
    17    23    26     2

The multiplication symbol, *, denotes the matrix multiplication involving inner products between rows and columns. Multiplying the transpose of a matrix by the original matrix also produces a symmetric matrix:

A'*A

ans =
   378   212   206   360
   212   370   368   206
   206   368   370   212
   360   206   212   378

The determinant of this particular matrix happens to be zero, indicating that the matrix is singular:

```
d = det(A)

d =
     0
```

The reduced row echelon form of A is not the identity:

R = rref(A)

R =
     1     0     0     1
     0     1     0    -3
     0     0     1     3
     0     0     0     0

Since the matrix is singular, it does not have an inverse. If you try to compute the inverse with

```
X = inv(A)
```

you will get a warning message:

Warning: Matrix is close to singular or badly scaled.
         Results may be inaccurate. RCOND = 9.796086e-018.

Roundoff error has prevented the matrix inversion algorithm from detecting exact singularity. But the value of rcond, which stands for reciprocal condition estimate, is on the order of eps, the floating-point relative precision, so the computed inverse is unlikely to be of much use.

The eigenvalues of the magic square are interesting:

e = eig(A)

e =
   34.0000
    8.0000
    0.0000
   -8.0000

One of the eigenvalues is zero, which is another consequence of singularity. The largest eigenvalue is 34, the magic sum. That is because the vector of all ones is an eigenvector:

v = ones(4,1)

v =
     1
     1
     1
     1

A*v

ans =
    34
    34
    34
    34

When a magic square is scaled by its magic sum,

```
P = A/34
```

the result is a doubly stochastic matrix whose row and column sums are all 1:

P =
    0.4706    0.0882    0.0588    0.3824
    0.1471    0.2941    0.3235    0.2353
    0.2647    0.1765    0.2059    0.3529
    0.1176    0.4412    0.4118    0.0294

Such matrices represent the transition probabilities in a Markov process. Repeated powers of the matrix represent repeated steps of the process. For our example, the fifth power

```
P^5
```

    0.2507    0.2495    0.2494    0.2504
    0.2497    0.2501    0.2502    0.2500
    0.2500    0.2498    0.2499    0.2503
    0.2496    0.2506    0.2505    0.2493

This shows that as 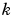approaches infinity, all the elements in the 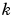th power, 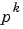, approach .

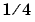Finally, the coefficients in the characteristic polynomial

```
poly(A)
```

are

```
     1   -34   -64  2176     0
```

This indicates that the characteristic polynomial

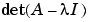
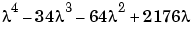
The constant term is zero, because the matrix is singular, and the coefficient of the cubic term is -34, because the matrix is magic!

Deleting Rows and Columns Arrays