Evaluating the Solution at Specific Points :: Differential Equations (Mathematics)

Mathematics

Evaluating the Solution at Specific Points

After obtaining and plotting the solution above, you might be interested in a solution profile for a particular value of t, or the time changes of the solution at a particular point x. The kth column u(:,k) (of the solution extracted in step 7) contains the time history of the solution at x(k). The jth row u(j,:) contains the solution profile at t(j).

Using the vectors x and u(j,:), and the helper function pdeval, you can evaluate the solution u and its derivative 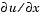partial derivative of u with respect to x at any set of points xout

[uout,DuoutDx] = pdeval(m,x,u(j,:),xout)

The example pdex3 uses pdeval to evaluate the derivative of the solution at xout = 0. See pdeval for details.

Changing PDE Integration Properties

The default integration properties in the MATLAB PDE solver are selected to handle common problems. In some cases, you can improve solver performance by overriding these defaults. You do this by supplying pdepe with one or more property values in an options structure.

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options)

Use odeset to create the options structure. Only those options of the underlying ODE solver shown in the following table are available for pdepe. The defaults obtained by leaving off the input argument options are generally satisfactory. Changing ODE Integration Properties tells you how to create the structure and describes the properties.

PDE Property Categories
Properties Category
Property Name

Error control
RelTol, AbsTol, NormControl

Step-size
InitialStep, MaxStep

**PDE Property Categories**
Properties Category	Property Name
Error control	`RelTol`, `AbsTol`, `NormControl`
Step-size	`InitialStep`, `MaxStep`

Solving PDE Problems Example: Electrodynamics Problem