Example: Electrodynamics Problem :: Differential Equations (Mathematics)

Mathematics

Example: Electrodynamics Problem

This example illustrates the solution of a system of partial differential equations. The problem is taken from electrodynamics. It has boundary layers at both ends of the interval, and the solution changes rapidly for small .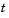

The PDEs are

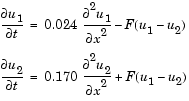
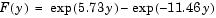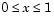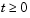where f (y) = exp(5.73 y) minus exp (-11.46 y) . The equations hold on an interval 0 less than or equal to x less than or equal to 1 for times t greater than or equal to 0 .

The solution 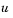satisfies the initial conditions

and boundary conditions

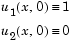
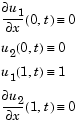
Note The demo pdex4 contains the complete code for this example. The demo uses subfunctions to place all required functions in a single M-file. To run this example type pdex4 at the command line. See PDE Solver Basic Syntax and Solving PDE Problems for more information.

Rewrite the PDE. In the form expected by pdepe, the equations are

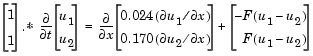
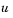The boundary conditions on the partial derivatives of have to be written in terms of the flux. In the form expected by pdepe, the left boundary condition is

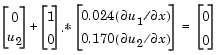
and the right boundary condition is

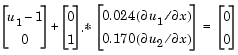
Code the PDE. After you rewrite the PDE in the form shown above, you can code it as a function that pdepe can use. The function must be of the form

```
[c,f,s] = pdefun(x,t,u,dudx)
```

where c, f, and s correspond to the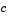

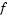, and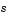

terms in Equation 5-3.

function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1]; 
f = [0.024; 0.17] .* DuDx; 
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];

Code the initial conditions function. The initial conditions function must be of the form

```
u = icfun(x)
```

The code below represents the initial conditions in the function pdex4ic.
- ```
function u0 = pdex4ic(x);
u0 = [1; 0]; 
```

Code the boundary conditions function. The boundary conditions functions must be of the form

```
[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)
```

The code below evaluates the components p(x,t,u)

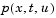and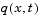

(Equation 5-5) of the boundary conditions in the function pdex4bc.

function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
pl = [0; ul(2)]; 
ql = [1; 0];     
pr = [ur(1)-1; 0]; 
qr = [0; 1];

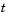Select mesh points for the solution. The solution changes rapidly for small . The program selects the step size in time to resolve this sharp change, but to see this behavior in the plots, output times must be selected accordingly. There are boundary layers in the solution at both ends of [0,1], so mesh points must be placed there to resolve these sharp changes. Often some experimentation is needed to select the mesh that reveals the behavior of the solution.

x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];

Apply the PDE solver. The example calls pdepe with m = 0, the functions pdex4pde, pdex4ic, and pdex4bc, and the mesh defined by x and t at which pdepe is to evaluate the solution. The pdepe function returns the numerical solution in a three-dimensional array sol, where sol(i,j,k) approximates the kth component of the solution, 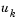, evaluated at t(i) and x(j).

m = 0;
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);

View the results. The surface plots show the behavior of the solution components.

u1 = sol(:,:,1);
u2 = sol(:,:,2);

figure
surf(x,t,u1)
title('u1(x,t)')
xlabel('Distance x')
ylabel('Time t')


figure
surf(x,t,u2)
title('u2(x,t)')
xlabel('Distance x')
ylabel('Time t')

Evaluating the Solution at Specific Points Selected Bibliography