Example: Solving a Fully Implicit ODE Problem :: Differential Equations (Mathematics)

Mathematics

Example: Solving a Fully Implicit ODE Problem

The following example shows how to use the function ode15i to solve the implicit ODE problem defined by Weissinger's equation

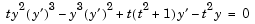
with the initial value 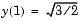. The exact solution of the ODE is

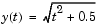
The example uses the function weissinger, which is provided with MATLAB, to compute the left-hand side of the equation.

Before calling ode15i, the example uses a helper function decic to compute a consistent initial value for 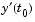. In the following call, the given initial value 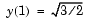is held fixed and a guess of 0 is specified for 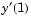. See the reference page for decic for more information.

t0 = 1;
y0 = sqrt(3/2);
yp0 = 0;
[y0,yp0] = decic(@weissinger,t0,y0,1,yp0,0);

You can now call ode15i to solve the ODE and then plot the numerical solution against the analytical solution with the following commands.

[t,y] = ode15i(@weissinger,[1 10],y0,yp0);
ytrue = sqrt(t.^2 + 0.5);
plot(t,y,t,ytrue,'o');

Solver for Fully Implicit ODEs Changing ODE Integration Properties