

| Mathematics |   |
Solver for Fully Implicit ODEs
The solver ode15i solves fully implicit differential equations of the form
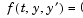
using the variable order BDF method. The basic syntax for ode15i is
|
A function that evaluates the left side of the differential equation of the form 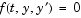 . . |
tspan |
A vector specifying the interval of integration, [t0,tf]. To obtain solutions at specific times (all increasing or all decreasing), use tspan = [t0,t1,...,tf]. |
y0, yp0 |
Vectors of initial conditions for 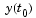 and and 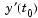 , respectively. The specified values must be consistent; that is, they must satisfy , respectively. The specified values must be consistent; that is, they must satisfy 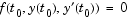 . Example: Solving a Fully Implicit ODE Problem shows how to use the function . Example: Solving a Fully Implicit ODE Problem shows how to use the function decic to compute consistent initial conditions. |
|
Optional integration argument created using the odeset function. See the odeset reference page for details. |
t |
Column vector of time points |
y |
Solution array. Each row in y corresponds to the solution at a time returned in the corresponding row of t. |
See the ode15i reference page for more information about these arguments.
 | Examples: Solving Explicit ODE Problems | Example: Solving a Fully Implicit ODE Problem |  |
© 1994-2005 The MathWorks, Inc.