Fitting a Curve to Data :: Function Functions (Mathematics)

Mathematics

Fitting a Curve to Data

This section gives an example that shows how to fit an exponential function of the form 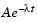A times e to power minus lamba times t to some data. The example uses the function fminsearch to minimize the sum of squares of errors between the data and an exponential function 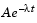for varying parameters A and 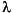lambda . This section covers the following topics.

Creating an M-file for the Example

To run the example, first create an M-file that

Accepts vectors corresponding to the x- and y-coordinates of the data
Returns the parameters of the exponential function that best fits the data

To do so, copy and paste the following code into an M-file and save it as fitcurvedemo in a directory on the MATLAB path.

function [estimates, model] = fitcurvedemo(xdata, ydata)
% Call fminsearch with a random starting point.
start_point = rand(1, 2);
model = @expfun;
estimates = fminsearch(model, start_point);
% expfun accepts curve parameters as inputs, and outputs sse,
% the sum of squares error for A * exp(-lambda * xdata) - ydata, 
% and the FittedCurve. FMINSEARCH only needs sse, but we want to 
% plot the FittedCurve at the end.
    function [sse, FittedCurve] = expfun(params)
        A = params(1);
        lambda = params(2);
        FittedCurve = A .* exp(-lambda * xdata);
        ErrorVector = FittedCurve - ydata;
        sse = sum(ErrorVector .^ 2);
    end
end

The M-file calls the function fminsearch, which find parameters A and lambda that minimize the sum of squares of the differences between the data and the exponential function A*exp(-lambda*t). The nested function expfun computes the sum of squares.

Running the Example

To run the example, first create some random data to fit. The following commands create random data that is approximately exponential with parameters A = 40 and lambda = .5.

xdata = (0:.1:10)'; 
ydata = 40 * exp(-.5 * xdata) + randn(size(xdata));

To fit an exponential function to the data, enter

[estimates, model] = fitcurvedemo(xdata,ydata)

This returns estimates for the parameters A and lambda,

```
estimates =

   40.1334    0.5025
```

and a function handle, model, to the function that computes the exponential function A*exp(-lambda*t).

Plotting the Results

To plot the fit and the data, enter the following commands.

plot(xdata, ydata, '*')
hold on
[sse, FittedCurve] = model(estimates);
plot(xdata, FittedCurve, 'r')
 
xlabel('xdata')
ylabel('f(estimates,xdata)')
title(['Fitting to function ', func2str(model)]);
legend('data', ['fit using ', func2str(model)])
hold off

The resulting plot displays the data points and the exponential fit.

Plot of data and best exponential fit on a single set of axes.

Minimizing Functions of Several Variables Setting Minimization Options