Cholesky Factorization :: Matrices and Linear Algebra (Mathematics)

Mathematics

Cholesky Factorization

The Cholesky factorization expresses a symmetric matrix as the product of a triangular matrix and its transpose

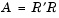
where R is an upper triangular matrix.

Not all symmetric matrices can be factored in this way; the matrices that have such a factorization are said to be positive definite. This implies that all the diagonal elements of A are positive and that the offdiagonal elements are "not too big." The Pascal matrices provide an interesting example. Throughout this chapter, our example matrix A has been the 3-by-3 Pascal matrix. Let's temporarily switch to the 6-by-6.

A = pascal(6)

A =
       1     1     1     1     1     1
       1     2     3     4     5     6
       1     3     6    10    15    21
       1     4    10    20    35    56
       1     5    15    35    70   126
       1     6    21    56   126   252

The elements of A are binomial coefficients. Each element is the sum of its north and west neighbors. The Cholesky factorization is

R = chol(A)

R =
     1     1     1     1     1     1
     0     1     2     3     4     5
     0     0     1     3     6    10
     0     0     0     1     4    10
     0     0     0     0     1     5
     0     0     0     0     0     1

The elements are again binomial coefficients. The fact that R'*R is equal to A demonstrates an identity involving sums of products of binomial coefficients.

Note The Cholesky factorization also applies to complex matrices. Any complex matrix which has a Cholesky factorization satisfies A' = A and is said to be Hermitian positive definite.

The Cholesky factorization allows the linear system

to be replaced by

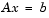
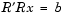
Because the backslash operator recognizes triangular systems, this can be solved in MATLAB quickly with

```
x = R\(R'\b)
```

If A is n-by-n, the computational complexity of chol(A) is O(n³), but the complexity of the subsequent backslash solutions is only O(n²).

Cholesky, LU, and QR Factorizations LU Factorization